高级光能
题目是什么意思啊？
求核心或排序规则
龙舟在2020-08-26 14:31:33追加了内容
大家快来呀，被我采纳福利多多
1.加豆子
2.男生专属壁纸免费赠送
ps：2选1
资深光能
来了！来了！
//Coding
#include <头文件（有两个）>
命名空间;
struct 数据类型名{
int 开始,
结束;
}a[101],p={注意！p.结束要赋值-1！赋值方法：p={开始的值，结束的值}};
计数器定义;
布尔 判断函数(就不告诉你)
就不告诉你（判断末尾）;
输入并排序
循环
超过了结束点
记录结束点
计数器加
输出
自己想。
我要30豆豆。
20个也可以。
你敢发1000000000000000000酷町豆我就敢发完整代码！
（部分完整代码：）
cout<<"完整代码"；
懂了么?
高级天翼
这个“2.男生专属壁纸免费赠送”是不是一些不好的图片？？
修练者
struct w{
int x,y;
}a[1010];
bool cmp(w a,w b)
{
return a.y<b.y;
}
int main()
{
int n,cnt=0,end=-1;
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i].x>>a[i].y;
sort(a+1,a+1+n,cmp);
for(int i=1;i<=n;i++){
if(a[i].x>end){
cnt++;
end=a[i].y;
}
}
cout<<cnt;
return 0;
}
资深光能
……
我是90分
我正在问老师。
你等等！
我预约一个采纳！
你的壁纸……不敢看
资深光能
给你一个图吧！
高级光能
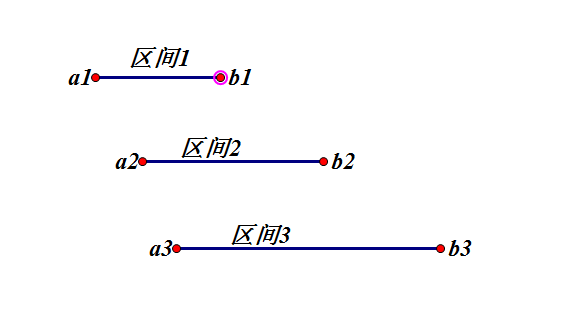
区间选点的问题大致可以描述为：
给定N个区间[a,b]，取尽量少的点，使得每个区间内都至少有一个点（不同区间内含的点可以重复）。
关于贪心算法的验证过程就不再赘述，现在思考一下贪心策略的制定。
对于区间[a1, b1] 、[a2, b2]、 [a3, b3] 来说，
如果想选择最少的点，那么必须选择每个区间的右端点，示意图如下：
当你每一次都选择区间的最右端，才能保证每一个选的点覆盖的范围都是最广泛的，也就是说选的点才是最少的。
和之前不相交区间的思考方法类似，把区间进行预处理，按照端点的大小排序（同样，按照右端点排序会好理解一点，但是左端点排序一样可以起到作用，初学者不必迷信右端点排序）。
预处理过后，求解策略的思路和求不相交区间相似，如果下一个区间的左端点不被覆盖，则答案+1，如下：
-
while(剩余区间的数目不为0) { if（找到符合条件的下一个区间） { 当前区间 = 下一个区间； 答案数+1； } 区间数--； }
代码：
请输入提取码，否则无法查看代码!
李致远在2020-08-27 08:58:16追加了内容
←提取码
中级守护
你的图是真不敢看
不然晚上鞭子挨定了
刘宇唐在2020-08-26 16:25:18追加了内容
毕竟这题我也不会写
中级守护
问下1000有木有创意写法（最好来点算法之类的）
看看有哪些技艺高超的秀儿
新手天翼
bool cmp(sh a,sh b){
if(a.zhong==b.zhong) {
return a.qi>b.qi;
}
return a.zhong<b.zhong;
}
排序的cmp给你
修练者
/*struct w{
int x,y;
}a[1010];
bool cmp(w a,w b)
{
if(a.x!=b.y)return a.x<b.y;
return a.y<b.y;
}
int main()
{
int n,cnt=0;
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i].x>>a[i].y;
sort(a+1,a+1+n,cmp);
for(int i=1;i<n;i++)
if(a[i].y<a[i+1].x)
cnt++;
cout<<cnt+1;
return 0;
}*/
