新手光能
中级启示者
具体实现流程：
1.输入
输入就不多说了，建议用邻接表存图，遍历时更方便。因为路径是双向的，因此要双向存边。在输入的同时统计所有路径的长度之和，以作为二分的右边界。
int ver[2*N],edge[2*N],Next[2*N],head[N],query[N];
void add(int x,int y,int z)
{
ver[++tot]=y,edge[tot]=z,Next[tot]=head[x],head[x]=tot;
}//邻接表插入操作
cin>>n;
for(int i=1;i<n;i++)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
add(x,y,z),add(y,x,z);
r+=z;//统计所有边的长度之和
}
cin>>m;
for(int i=1;i<=m;i++)
scanf("%d",&query[i]);//输入军队
2. 树上倍增预处理
这个步骤的实现和求LCA基本相同，用到了二进制拆分的思想。关于树上倍增法求LCA，不懂的可以点击食用（虽然和这题没有太大关系），接下来也会详细讲解。
在这里用f_{i,j}fi,j存储ii节点的第2^j2j个祖先的节点编号，dist_{i,j}disti,j存储ii节点到它的第2^j2j个祖先的路径长度。在预处理过程中同时也处理出每个节点的深度，用d_idi表示。
以上三个数组的值可以通过递推得出，对于ff数组和distdist数组，有以下递推式：
f[i][j]=f[f[i][j-1]][j-1];
dist[i][j]=dist[i][j-1]+dist[f[i][j-1]][j-1];
这个递推式根据数组的定义很容易推出，请读者自行思考。
d数组的递推式就不多说了，待下面给出实现过程时读者自然清楚。
本文这个步骤用bfs实现，当然用dfs实现也可以。
接下来给出具体实现过程：
- 建立一个空队列，并将根节点入队，同时存储根节点的深度
- 取出队头，遍历其所有出边。由于存储的时候是按照无向图存储，因此要进行深度判定，对于连接到它父亲节点的边，直接continue即可。记当前路径的另一端节点为yy，处理出yy的dd、ff、distdist三个数组的值，然后将yy入队。
- 重复第2步，直到队列为空
ff数组和distdist数组的递推初值是多少呢？显然，f_{i,0}fi,0表示的就是ii节点的父亲节点，因此可以直接得出f_{i,0}fi,0和dist_{i,0}disti,0的值，其余为0，接下来进行递推就可以了。
int d[N],f[N][20];
ll dist[N][20];
queue<int> q;
t=log2(n)+1;//f数组和dist数组第二维下标的最大值
void bfs()
{
q.push(1);
d[1]=1;
while(q.size())
{
int x=q.front();q.pop();
for(int i=head[x];i;i=Next[i])//遍历x的出边
{
int y=ver[i];
if(d[y])
continue;//若深度小于当前节点，说明是当前节点的父节点
d[y]=d[x]+1;//这步不用解释了吧
f[y][0]=x,dist[y][0]=edge[i];//递推初值
for(int j=1;j<=t;j++)
{
f[y][j]=f[f[y][j-1]][j-1];
dist[y][j]=dist[y][j-1]+dist[f[y][j-1]][j-1];
}//递推
q.push(y);
}
}
}
3. 二分答案
经过预处理后，就开始二分答案了。二分时，若当前的时间限制满足题意，则更新答案。这个步骤比较简单，就不多说了。
while(l<=r)
{
mid=(l+r)>>1;
if(check(mid))
{
r=mid-1;
ans=mid;
ok=1;//有解标记
}
else
l=mid+1;
}
下面给出check函数的实现
4. 上移军队并存储闲置军队
与求LCA类似，利用树上倍增实现上移。用二进制拆分的思想，具体来说，就是依次尝试向上走2^{logn},...,2^1,2^02logn,...,21,20步，并保证终点在根节点之前，且时间不超过当前的时间限制。
将军队上移到根节点的子节点或者能够达到的最浅节点后，若该军队还能向上到达根节点，说明它还有转移到其它子树去驻扎的可能，因此将它记为暂时闲置，用一个二元组存储起来；否则就将该军队驻扎在当前节点，并将当前节点标记为已驻扎。
二元组排序时会以第一维的大小排序，因此在这里第一维存储该军队到达根节点后剩余的时间，第二维存储该军队当前所在的节点编号。
int ctot=0;
pair<ll,int> h[N];
bool sta[N];
//lim表示当前的时限，即check函数传入的参数
for(int i=1;i<=m;i++)
{
ll x=query[i],cnt=0;//cnt统计时间花费
for(int j=t;j>=0;j--)//从logn到0枚举
if(f[x][j]>1 && cnt+dist[x][j]<=lim)//若终点在根节点之前且不会超过时限
{
cnt+=dist[x][j];
x=f[x][j];
}
if(f[x][0]==1 && cnt+dist[x][0]<=lim)//若当前节点为根节点的子节点且该军队可以在时限内到达根节点
h[++ctot]=make_pair(lim-cnt-dist[x][0],x);//存储闲置军队
else
sta[x]=1;//已驻扎标记
}
5. dfs寻找路径未被驻扎的叶子节点
这里的思想比较简单，从每个根节点的子节点开始搜索，若搜索时遇到已驻扎节点，则返回1；若一直搜索到某个叶子节点都没有遇到已驻扎节点，则说明根节点的这个子节点需要军队驻扎，返回0。
和上面的bfs预处理一样，当遇到连接父节点的边时，continue即可。
dfs查找结束后，存储需要根节点的需要被驻扎的子节点。
bool need[N];
bool dfs(int x)
{
bool pson=0;//判断是否为叶子节点
if(sta[x])
return 1;//若当前节点已被驻扎，则返回1
for(int i=head[x];i;i=Next[i])//遍历x的出边
{
int y=ver[i];
if(d[y]<d[x])
continue;//遇到父节点
pson=1;//若有一条不是连接着父节点的边，说明不是叶子节点
if(!dfs(y))//若某个子节点搜索时遇到路径未被驻扎的叶子节点，直接返回0
return 0;
}
if(!pson)//当前节点是叶子节点且未被驻扎
return 0;
return 1;//没有遇到路径未被驻扎的叶子节点，返回1
}
for(int i=head[1];i;i=Next[i])//遍历根节点的子节点
if(!dfs(ver[i]))//若需要被驻扎
need[ver[i]]=1;
6. 对根节点的需要被驻扎的子节点进行初步处理
在讲解这个步骤之前先说明一个引理：对于第5步中需要被驻扎的节点，若该节点上有军队停留，则对于这些军队中剩余时间最小的军队，若该军队的剩余时间不足够令它从根节点再返回现在停留的节点，则直接驻扎在该节点是最优的。
为什么呢？因为该军队无法从当前的节点到达根节点再返回，说明若它驻扎在根节点的其它子树，只能驻扎在一个到根节点的距离小于当前节点到根节点的距离的节点。而这个节点所有剩余时间比它多的军队一定也可以去驻扎，甚至还可能驻扎到其它更多的节点。因此不如让剩余时间多的节点去驻扎，而自己留在当前节点即可。
身为一个蒟蒻，也没办法给出多么严密的解释，不过总之，上面给出的引理可以证明是成立的。因此对于任意一个需要被驻扎的节点，若它上面停留着一支军队不能到达根节点并返回该节点，则令其驻扎在该节点；另外的，因为一个节点只需要一支军队驻扎，因此我们在这里选择剩余时间最小的节点。所以在处理前要先将hh数组按照剩余时间从小到大排序。
对于处理过后仍闲置的军队，将它们的剩余时间存储起来备用。因为此时我们已经不关心它当前停留在哪个节点，因此只要存储剩余时间就好。
int atot=0;
ll tim[N];
sort(h+1,h+ctot+1);//排序，二元组按照第一维大小排序
for(int i=1;i<=ctot;i++)//遍历所有闲置的军队
if(need[h[i].second] && h[i].first<dist[h[i].second][0])//若该军队所处的节点需要被驻扎且该军队无法到达根节点并返回
need[h[i].second]=0;//去除标记
else
tim[++atot]=h[i].first;//存储军队的剩余时间
7. 找到仍需要被驻扎的节点并存储
经过第6步的初步处理，可能还有一些节点需要被驻扎，此时遍历一遍根节点的子节点，找到这些节点并存储起来备用。与第6步相同，这里只要存储节点到根节点的距离就可以了，不必存储节点编号。
int btot=0;
ll ned[N];
for(int i=head[1];i;i=Next[i])
if(need[ver[i]])//如果仍需要被驻扎
ned[++btot]=dist[ver[i]][0];
8. 利用贪心策略完成最后的匹配
这里有一个贪心策略：对于现在闲置的军队和需要被驻扎的节点，让剩余时间小的军队优先驻扎在距离根节点近的节点，这样可以保证决策最优。匹配过后，若所有需要被驻扎的节点都已有军队驻扎，则说明当前的时限可行；反之则不可行。
if(atot<btot)
return 0;//如果剩余的军队比需要被驻扎的节点还少，显然不可行，直接返回0
sort(tim+1,tim+atot+1),sort(ned+1,ned+btot+1);//分别对军队的剩余时间和节点到根节点的距离进行升序排序
int i=1,j=1;//指针
while(i<=btot && j<=atot) //扫描整个tim和ned数组
if(tim[j]>=ned[i])//若可行
{
i++,j++;//都扫描到下一位
}
else
j++;//否则扫描下一支军队
if(i>btot)//说明所有需要被驻扎的节点都已被驻扎
return 1;
return 0;
至此，check函数就愉快地结束了。
9. 特判并输出
题目中要求对无解的情况进行特判，若二分时没有任何一个时限满足条件，自然就说明无解。否则输出答案即可。虽然并没有无解的数据
if(!ok)
cout<<-1;
else
cout<<ans;
完结撒花！
整道题目主要还是细节多，在写这类较为复杂的题目时一定要注意细节，防止会写的题爆零。
如果以上讲解没有听懂，可以借助下面这组数据更详细地了解：
10 5
2 1 3
2 3 4
1 4 7
5 1 9
6 1 2
4 7 9
7 8 8
9 8 8
1 10 2
2 8 5 4 2
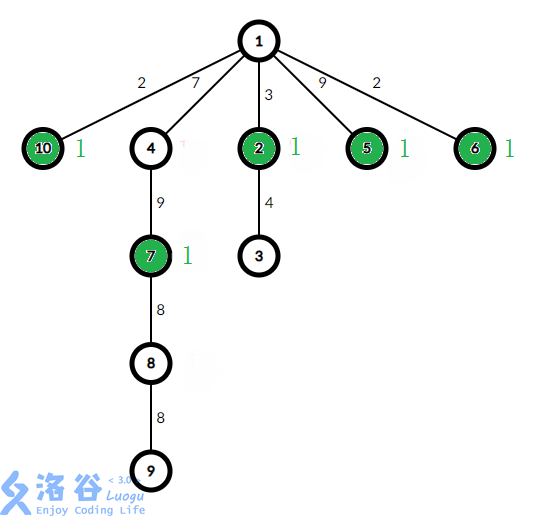
这组数据构造出来就长这个样子：
假设我们当前二分到的时间限制为9，模拟上面的步骤进行一遍。
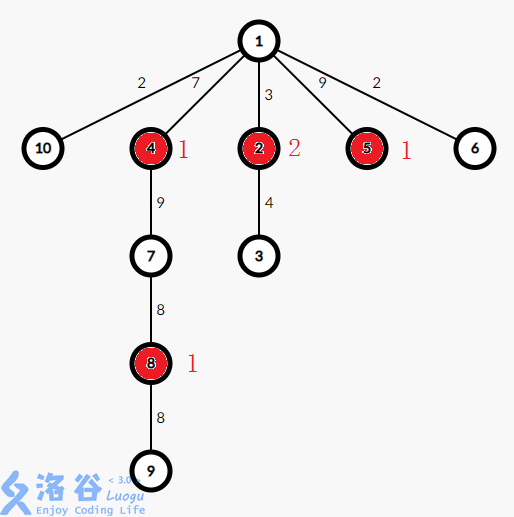
- 上移军队：只有处于节点8的军队上移到了节点7，其余节点由于都在根节点的子节点上，不动。
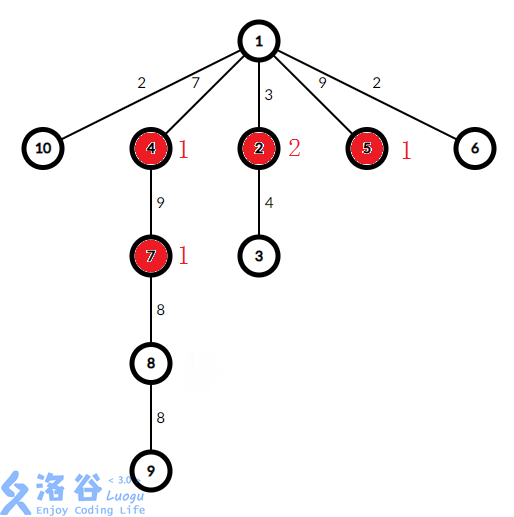
- 找出闲置军队与需要被驻扎的节点。显然，闲置军队为目前处于4、2、5节点上的4支军队，需要被驻扎的节点为10、2、5、6节点。
- 初步处理这些数据。由于5号节点上的军队无法到达根节点再返回，且该节点需要被驻扎，因此该军队驻扎在五号节点；同理，7号节点上的军队驻扎在七号节点。
-
找出目前的闲置军队和需要被驻扎的节点。剩余的闲置军队为目前处于4、2节点上的3支军队，需要被驻扎的节点为2、6、10号节点。
-
利用贪心策略进行最后的匹配。最后，4号节点上的军队驻扎到6号节点，2号节点上的两支军队分别驻扎到2、10号节点。该方案是可行的。
高级天翼
我发现了一个神奇的东西
这是哪位“dalao”，我就不说了
中级守护
你错误代码呢？
新手天翼
shui
缔造者之神
顶
高级启示者
@夏雨轩 您别水了，有些人他就是一点思路都没有，但他一旦有了灵感，就马上通了
新手光能
顶
