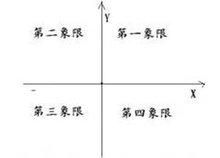
右上的叫第一象限(+,+)
左上的叫第二象限 (-,+)
左下的叫第三象限(-,-)
右下的叫第四象限(+,-)
在轴上的点不属于任何象限.
平面直角坐标系又称为笛卡尔坐标系,由一个原点(坐标为(0,0))和两个通过原点的、相互垂直的坐标轴构成(见图2-11)。其中,水平方向的坐标轴为X轴,以向右为其正方向;垂直方向的坐标轴为Y轴,以向上为其正方向。平面上任何一点P都可以由X轴和Y轴的坐标所定义,即用一对有序实数对(x,y)来定义并定位一个点。
性质
1.第一象限中的点的横坐标(x)大于0,纵坐标(y)大于0。
2.第二象限中的点的横坐标(x)小于0,纵坐标(y)大于0。
3.第三象限中的点的横坐标(x)小于0,纵坐标(y)小于0。
4.第四象限中的点的横坐标(x)大于0,纵坐标(y)小于0。
坐标数值
第一象限:(正,正),(+,+)横纵坐标同号,记作xy>0
第二象限:(负,正 ),(﹣,+)横纵坐标异号,记作xy<0
第三象限:(负,负),(﹣,﹣)横纵坐标同号,记作xy>0
第四象限:(正,负),(+,﹣)横纵坐标异号,记作xy<0
x轴正方向:(+,0)
x轴负方向:(-,0)
y轴正方向:(0,+)
y轴负方向:(0,-)
*注:在坐标轴上的点,不在象限内。
坐标角度
可以看该角的终边上的任意一点的坐标(x,y)
x>0,y>0时在第一象限
x<0,y>0时在第二象限
x<0,y<0时在第三象限
x>0,y<0时在第四象限
也可以根据角度来看,设角度为α,
2kπ<α<2kπ+π/2时,在第一象限
2kπ+π/2<α<2kπ+π时,在第二象限
2kπ+π<α<2kπ+3π/2时,在第三象限
2kπ+3π/2<α<2kπ+2π时,在第四象限
k为任意整数,另外这里我用的是弧度制,π=180度
发现历史
笛卡尔和笛卡尔坐标系的产生
据说有一天,法国哲学家、数学家笛卡尔生病卧床,病情很重,尽管如此他还反复思考一个问题:几何图形是直观的,而代数方程是比较抽象的,能不能把几何图形与代数方程结合起来,也就是说能不能用几何图形来表示方程呢?要想达到此目的,关键是如何把组成几何图形的点和满足方程的每一组“数”挂上钩,他苦苦思索,拼命琢磨,通过什么样的方法,才能把“点”和“数”联系起来。突然,他看见屋顶角上的一只蜘蛛,拉着丝垂了下来,一会功夫,蜘蛛又顺着丝爬上去,在上边左右拉丝。
蜘蛛的“表演”使笛卡尔的思路豁然开朗。他想,可以把蜘蛛看做一个点,它在屋子里可以上、下、左、右运动,能不能把蜘蛛的每个位置用一组数确定下来呢?他又想,屋子里相邻的两面墙与地面交出了三条线,如果把地面上的墙角作为起点,把交出来的三条线作为三根数轴,那么空间中任意一点的位置就可以用这三根数轴上找到有顺序的三个数。反过来,任意给一组三个有顺序的数也可以在空间中找出一点P与之对应,同样道理,用一组数(x、y)可以表示平面上的一个点,平面上的一个点也可以有用一组两个有顺序的数来表示,这就是坐标系的雏形。
直角坐标系的创建,在代数和几何上架起了一座桥梁,它使几何概念用数来表示,几何图形也可以用代数形式来表示。由此笛卡尔在创立直角坐标系的基础上,创造了用代数的方法来研究几何图形的数学分支——解析几何, 他大胆设想:如果把几何图形看成是动点的运动轨迹,就可以把几何图形看成是由具有某种共同特征的点组成的。举一个例子来说,我们可以把圆看作是动点到定点距离相等的点的轨迹,如果我们再把点看作是组成几何图形的基本元素,把数看作是组成方程的解,于是代数和几何就这样合为一家人了。
象限
 来,乐呵乐呵!!!
来,乐呵乐呵!!!

邵逸儒在2018-02-20 19:18:37追加了内容
定义 a,b;
输入 a,b;
如果x>0&&y>0:输出1;
如果x<0&&y>0:输出2;
如果x<0&&y<0:输出3;
如果x>0&&y<0:输出4;

象限:

然后判断正负
马佳滢在2018-02-20 17:42:44追加了内容
搞懂象限问题后,就会写啦!!!
//定义 x,y,c;
// 输入x、y;
// 判断(如果x大于0并且y大于0){ //x正,y正,第一象限
// c赋值1;
// }否则 判断(x小于0并且y大于0){ //x负,y正,第二象限
// c赋值2;
// }否则 判断(x小于0并且y小于0){ //x负,y负,第三象限
// c赋值3;
// }否则 判断(x大于0并且y小于0){ //x正,y负,第四象限
// c赋值4;
// }
// 输出c;
// 返回值 0;
scanf("%d %d",&x,&y);
if(x>0&&y>0)
d=1;
if(x<0&&y>0)
d=2;
if(x<0&&y<0)
d=3;
if(x>0&&y<0)
d=4;
printf("%d\n",d);
if(x>0&&y>0)
cout<<1;
if(x<0&&y>0)
cout<<2;
if(x<0&&y<0)
cout<<3;
if(x>0&&y<0)
cout<<4;
//以下为科普知识,仅供参考
象限(Quadrant)是平面直角坐标系(笛卡尔坐标系)中里的横轴和纵轴所划分的四个区域,每一个区域叫做一个象限。象限以原点为中心,x,y轴为分界线。右上的称为第一象限,左上的称为第二象限,左下的称为第三象限,右下的称为第四象限。坐标轴上的点不属于任何象限。[1]
中文名
象限
外文名
Quadrant
创立人
笛卡尔
主要应用
分 类
第一、二、三、四象限
目录
定义
编辑
象限,英文为Quadrant,原意是1/4圆等分的意思。象限即直角坐标系,创立人是笛卡儿。主要应用于三角学和复数的阿根图坐标系(复平面)中。在平面直角坐标系中,平面被横轴与纵轴划分为四个区域,即为四个象限。象限以原点为中心,以横轴、纵轴为分界线,按逆时针方向由右上方开始分为I、II 、III 、 IV四个象限,原点和坐标轴不属于任何象限。[2]
性质
编辑
坐标
记

是象限中的一点
①第一象限中的点:

②第二象限中的点:

③第三象限中的点:

④第四象限中的点:

值得注意的是原点和坐标轴上的点不属于任何象限。
角度
记角

是始边落在

轴正方向,终边按逆时针方向落在坐标平面内的象限角
①第一象限角:

②第二象限角:

③第三象限角:

④第四象限角:

其中,

。
象限(Quadrant)是平面直角坐标系(笛卡尔坐标系)中里的横轴和纵轴所划分的四个区域,每一个区域叫做一个象限。象限以原点为中心,x,y轴为分界线。右上的称为第一象限,左上的称为第二象限,左下的称为第三象限,右下的称为第四象限。坐标轴上的点不属于任何象限。[1]
https://baike.baidu.com/item/%E8%B1%A1%E9%99%90/10223942?fr=aladdin
还是复制了一下;
坐标
记

是象限中的一点
①第一象限中的点:

②第二象限中的点:

③第三象限中的点:

④第四象限中的点:

值得注意的是原点和坐标轴上的点不属于任何象限。
角度
记角

是始边落在

轴正方向,终边按逆时针方向落在坐标平面内的象限角
①第一象限角:

②第二象限角:

③第三象限角:

④第四象限角:

其中,

。
象限的创建和意义
据说有一天,法国哲学家、数学家笛卡儿生病卧床,病情很重。尽管如此,他还反复思考一个问题:几何图形是直观的,而代数方程是比较抽象的,能不能把几何图形与代数方程结合起来,也就是说能不能用几何图形来表示方程呢?
要想达到此目的,关键是如何把组成几何图形的点和满足方程的每一组“数”挂上钩。他苦苦思索,拼命琢磨,通过什么样的方法,才能把“点”和“数”联系起来。突然,他看见屋顶角上的一只蜘蛛,拉着丝垂了下来,一会儿工夫,蜘蛛又顺着丝爬上去,在上边左右拉丝。蜘蛛的‘“表演”使笛卡儿的思路豁然开朗。
他想,可以把蜘蛛看做一个点,它在屋子里可以上、下、左、右运动,能不能把蜘蛛的每个位置用一组数确定下来呢?他又想。屋子里相邻的两面墙与地面交出了三条线,如果把地面上的墙角作为起点,把交出来的二条线作为三根数轴,那么空间中任意一点的位置就可以用这三根数轴上找到有顺序的三个数。反过来,任意给一组三个有顺序的数也可以在空间中找出一点F与之对应,同样道理,用一组数(x ,y)可以表示平面上的一个点,平面上的一个点也可以有用一组两个有顺序的数来表示,这就是坐标系的雏形。
直角坐标系的创建,在代数和几何之间架起了一座桥梁,它使几何概念用数来表示,几何图形也可以用代数形式来表示。由此笛卡儿在创立直角坐标系的基础上,创造了用代数的方法来研究几何图形的数学分支——解析几何。
他大胆设想:如果把几何图形看成是动点的运动轨迹,就可以把几何图形看成是由具有某种共同特征的点组成的。举一个例子来说,我们可以把圆看作是动点到定点距离相等的点的轨迹,如果我们再把点看作是组成几何图形的基本元素,把数看作是组成方程的解,于是代数和几何就合二为一了。[2]
栾峻岩在2018-02-20 22:53:02追加了内容
这道题呵~是这样写滴~
if (第一象限满足) cout<<1;
else if (第二象限满足) cout<<2;
else if (第三象限满足) cout<<3;
else cout<<4;