由于大号的豆豆没了,我只能用小号发讲解了

-------------------------------------------------------------------------------------------
最短路径:floyd穷举 & djksl算法 & SPFA算法
floyd穷举:3道循环---O(n^3)===============
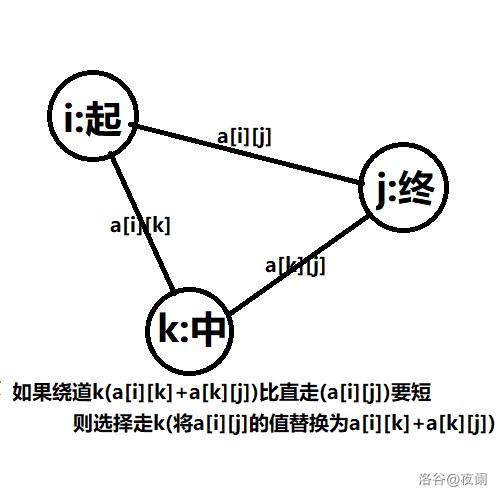
分别穷举中间点,起点,终点,如果起点和终点之间通过中间点更近则刷新 使用邻接矩阵,求出任意一点和其他所有点之间的最短路径
初始化:将所有点之间的长度设为无穷大,将对角线设为0//自己到自己路径长度为0
step1:穷举中间点---k
step2:穷举起点-----i
step3:穷举终点-----j
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(i==j||j==k||k==i)continue;//如果起点,终点,中间点相同,则跳过
else if(a[i][j]>a[i][k]+a[k][j])
a[i][j]=a[i][k]+a[k][j]//如果通过中间点更近则走中间点
}
}
}djskl算法->单源最短路径===============
求一个点到所有其他点之间的最短路径,时间复杂度O(n-1) 设dis[i]表示所设置的源点到i点之间的最短路径 将已经求出来最短路径的点放到集合中
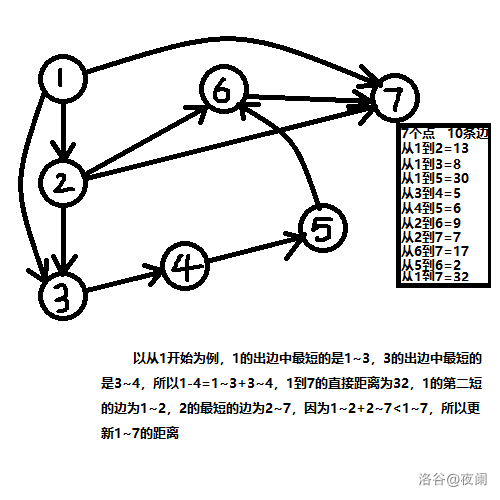
具体步骤:
step1:设置源点s,dis[s]=0;
step2:穷举s的出边,找到所有出边中的最小值i,将i放到T集合中(标记flag)
step3:以i为临时源点,找到i的出边中的最小值j,可得s->j的最小值=s->i->j的值使用邻接矩阵/前向星都可以
#include<iostream>
using namespace std;
/*
算法法思想:S=v0,循环n-1次,
第一步:求出 dis[]数组(表示顶点v0到
其他所有顶点的最短路径,初始化为v0的
直接出边,没有边的为∞)的最小值对
应的顶点k;第二步:把k加到S中(作
标记);第三步:用k作为中间点去刷
新dis[]数组 (dis[j]>dis[k]+a[k][j]);
测试数据:
7 10
1 2 13
1 3 8
1 5 30
3 4 5
4 5 6
2 6 9
2 7 7
6 7 17
5 6 2
1 7 32
七个点,十条边,起点,终点,权值
*/
struct node{int to,w,next;};//
node bian[10001];
int n,m,cnt;
int head[10001];//前向星索引表
int dis[10001];//dis[3]=源点到3的最短距离
int flag[10001];//标记是否已经在集合T中
void add(int x,int y,int w){//x:起点,y:终点,w:权值
cnt++;//cnt:边的总条数
bian[cnt].to=y;//终点赋值
bian[cnt].w=w;//权值赋值
bian[cnt].next=head[x];//当前下一条边的序号设置
head[x]=cnt;//头插法:x的第一条出边修改为当前边序号设置
}
void djskl(int x){//求源点x到其他点的最短距离
int i,j,k,min1,y;//每次求dis距离的最小值,和对应的顶点k
for(i=1;i<=n;i++)dis[i]=987654321;//最短距离初始化为无穷大
dis[x]=0;//自己到自己为0
flag[x]=1;//把源点x加入T集合中
for(k=head[x];k;k=bian[k].next)//k:x出边的序号,找x的出边
dis[bian[k].to]=bian[k].w;
for(i=1;i<=n-1;i++){//T中有一个x,要穷举找点n-1次
min1=987654321;y=0;//第一步:每次找dis的最小值对应的顶点y,把y加入T中
for(j=1;j<=n;j++){
if(dis[j]<min1&&flag[j]==0){
min1=dis[j];y=j;//刷新最短距离,记下标
}
}
flag[y]=1;//第二步:用新增加的点y去刷新dis
for(k=head[y];k;k=bian[k].next){//找y的直接出边
if(dis[bian[k].to]>dis[y]+bian[k].w){
dis[bian[k].to]=dis[y]+bian[k].w;
}
}
}
cout<<x<<"到其他点的最短距离:"<<endl;
for(i=1;i<=n;i++)cout<<x<<"-->"<<i<<":"<<dis[i]<<endl;
}
int main(){
int x,y,w;
cin>>n>>m;//n个点,m条边
for(int i=1;i<=m;i++){
cin>>x>>y>>w;//起点,终点,权值
add(x,y,w);
}
djskl(1);
return 0;
}SPFA算法=====================
--------------------------------学了这个上面的都没用的算法
SPFA:求单源最短路径的一维算法
基本思想:队列+BFS
step1:初始化,将dis[i]全部置为无穷大,将dis[自己]置为1//直接相临的点也置为无穷大而不是边长
step2:将源点入队,当队列不空时持续BFS
BFS:取出队首,清空队首标记(队首可能再次入队),
将队首的直接临边(t)入队并标记(防止队中同时出现多个同一点),
如果通过队首到达t比直接到达t要更近,则改变源点到t的距离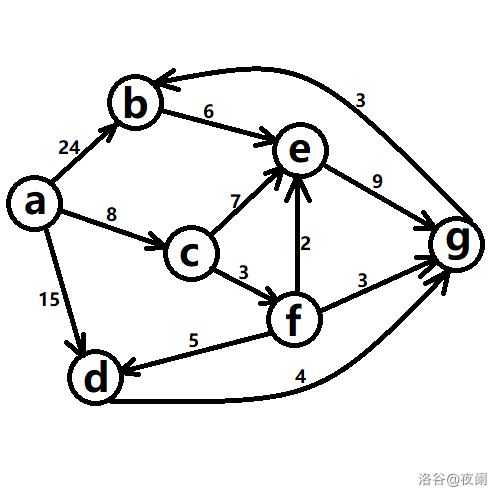
以上图为例,求源点a到g的最短路径:
首先建立起始点a到其余各点的最短路径表格
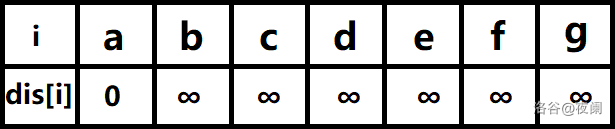
首先源点a入队,当队列非空时:
1、队首元素(a)出队,对以a为起始点的所有边的终点依次进行松弛操作(此处有b,c,d三个点),此时路径表格状态为:
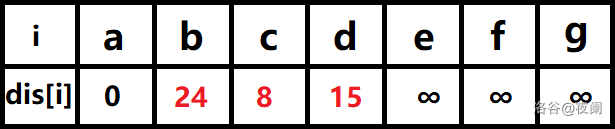
在松弛时三个点的最短路径估值变小了,而这些点队列中都没有出现,这些点需要入队,此时,队列中新入队了三个结点b,c,d
队首元素b点出队,对以b为起始点的所有边的终点依次进行松弛操作(此处只有e点),此时路径表格状态为:dje>dib+bw[i][je]
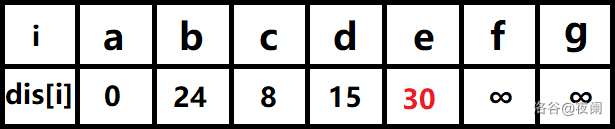
在最短路径表中,e的最短路径估值也变小了,e在队列中不存在,因此e也要入队,此时队列中的元素为c,d,e
队首元素c点出队,对以c为起始点的所有边的终点依次进行松弛操作(此处有e,f两个点),此时路径表格状态为:
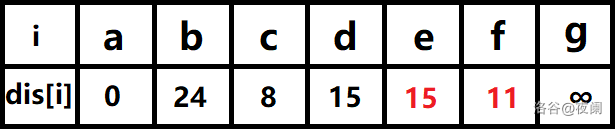
在最短路径表中,e,f的最短路径估值变小了,e在队列中存在,f不存在。因此e不用入队了,f要入队,此时队列中的元素为d,e,f
队首元素d点出队,对以d为起始点的所有边的终点依次进行松弛操作(此处只有g这个点),此时路径表格状态为:
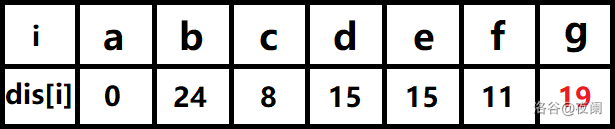
在最短路径表中,g的最短路径估值变小了,g在队列中不存在,因此g要入队,此时队列中的元素为e,f,g
队首元素e点出队,对以e为起始点的所有边的终点依次进行松弛操作(此处只有g这个点),此时路径表格状态为:

在最短路径表中,g的最短路径估值没有变小(松弛不成功),没有新结点入队,队列中元素为f,g
队首元素f点出队,对以f为起始点的所有边的终点依次进行松弛操作(此处有d,e,g三个点),此时路径表格状态为:

在最短路径表中,e,g的最短路径估值又变小,队列中无e点,e入队,队列中存在g这个点,g不用入队,此时队列中元素为g,e
队首元素g点出队,对以g为起始点的所有边的终点依次进行松弛操作(此处只有b点),此时路径表格状态为:
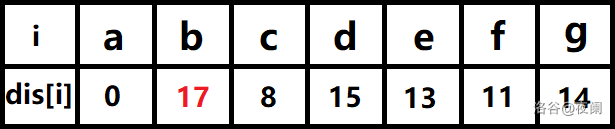
在最短路径表中,b的最短路径估值又变小,队列中无b点,b入队,此时队列中元素为e,b
队首元素e点出队,对以e为起始点的所有边的终点依次进行松弛操作(此处只有g这个点),此时路径表格状态为:

在最短路径表中,g的最短路径估值没变化(松弛不成功),此时队列中元素为b
队首元素b点出队,对以b为起始点的所有边的终点依次进行松弛操作(此处只有e这个点),此时路径表格状态为:d[j]<=d[i]+w[i][j] d[j]-d[i]<=w[i][j]

在最短路径表中,e的最短路径估值没变化(松弛不成功),此时队列为空了
最终a到g的最短路径为 14
代码:
#include<iostream>
using namespace std;
/*
SPFA:求单源最短路径,可以带负权,不能带负环
得到一维数组
*/
int q[10001],tou=1,wei=1;//队列
int ving[10001];//标记在不在队列中
int dis[10001];//dis[i]表示源点到i的最短路
int n,m;//n个点,m条边
//前向星
struct node{int w,to,next;};
int cnt=0,head[10001];//cnt表示边的条数
node bian[10001];
void add(int x,int y,int w){
cnt++;
bian[cnt].to=y;
bian[cnt].w=w;
bian[cnt].next=head[x];
head[x]=cnt;
}
void push(int x){q[wei++]=x;}//入队
int pop(){//出队
if(tou==wei)return 987654321;
return q[tou++];//出队头,头指针后移
}
void spfa(int x){//求源点到其他所有点的最短距离
int j,y,t,k;
for(int i=1;i<=n;i++)//初始化,自己到自己为0,到其他点为无穷大,不需要赋值直接出边
dis[i]=987654321;
dis[x]=0;
push(x);//源点入队列
ving[x]=1;//标记
while(tou!=wei){//队列不为空时
y=pop();
ving[y]=0;//清空队列标记
if(y==-987654321)break;//队列为空
for(k=head[y];k;k=bian[k].next){//k是第几条边
if(dis[y]+bian[k].w<dis[bian[k].to]){//距离变短
dis[bian[k].to]=dis[y]+bian[k].w;
if(ving[bian[k].to]==0){//t不在队列中
push(bian[k].to);//入队
ving[bian[k].to]=1;//做标记
}
}
}
}
for(int i=1;i<=n;i++)
cout<<dis[i]<<' ';
cout<<endl;
}
int main(){
int x,y,w;
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>x>>y>>w;
add(x,y,w);
}
spfa(1);
return 0;
}




