问题标题: 酷町堂：算法讲解5：生成树综合

生成树，并查集，最小生成树

生成树：在一个n个顶点的无向连通图里构建一棵，边的条数为n-1

并查集：->集合(树)的合并与查找

[1]集合(树)的查找：查找集合(树)的总根

查找方法：递归

step1：定义：自己为x号节点，fu[]数组表示父节点，
    fu[i]表示i的父节点的序号
step2：查找：查找自己的父节点fu[x]，
    如果父节点==自己就表示自己是**的，直接返回(见下面并查集的合并初始化)
    如果找到了父节点就递归，查找自己父节点的父节点，直到找到根节点(根节点的父节点是自己)
step3：优化：为了防止树的层数太大，每次递归将该节点的父节点设置为所在那棵树的根节点上

-------代码分割线(代码及其简单)

int bcj(int x){//寻找x节点的父节点
    if(fu[x]==x)return x;//找到根节点了或该节点是**的
    fu[x]=bcj(fa[x]);//优化，将父节点设置为根节点
    return fu[x]; //返回找到的父节点
}

[2]合并方法：查找总根+链接

step1：定义：自己为x号节点，fu[]数组表示父节点，
    fu[i]表示i的父节点的序号
step2：查找：查找自己的父节点fu[x]，
    如果父节点==自己就表示自己是**的，直接返回(见下面并查集的合并初始化)
    如果找到了父节点就递归，查找自己父节点的父节点，直到找到根节点(根节点的父节点是自己)
step3：优化：为了防止树的层数太大，每次递归将该节点的父节点设置为所在那棵树的根节点上

-------代码分割线(代码及其简单)

int bcj(int x){//寻找x节点的父节点
    if(fu[x]==x)return x;//找到根节点了或该节点是**的
    fu[x]=bcj(fa[x]);//优化，将父节点设置为根节点
    return fu[x]; //返回找到的父节点
}

最小生成树吗

概念:使生成树的所有边的权值总和最小

[方法1]：并查集最小生成树：

基本思想：[加边]，给定一张图，把图中各条边按照权值大小从小到大排序，依次判断能否加边直到有n-1条边加进了树中

能否加边关键看边两端的点是否在同一棵树内，在同一棵树内就不能加边

代码：

#include<iostream>
#include<algorithm>
using namespace std;
struct node{int x,y,w;};
node bian[200001];
int fa[200001],sum,num;
int bcj(int x){
    if(fa[x]==x)return x;
    fa[x]=bcj(fa[x]);
    return fa[x]; 
}
bool cmp(node x,node y){
    if(x.w<y.w)return 1;
    else return 0; 
}
int start[200001],enm[200001];
int main(){
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        int x,y,z;
        cin>>x>>y>>z;
        bian[i].x=x;
        bian[i].y=y;
        bian[i].w=z;
        start[x]++;
        enm[y]++;
    }
    for(int i=1;i<=m;i++){
        if(start[i]==0&&enm[i]==0){
            cout<<"orz"; 
        }
    }
    sort(bian+1,bian+1+m,cmp);
    for(int i=1;i<=n;i++)
        fa[i]=i;
//  for(int i=1;i<=m;i++)
//      cout<<bian[i].x<<"---"<<bian[i].y<<' '<<bian[i].w<<endl;
    for(int i=1;i<=m;i++){
        int x=bian[i].x;
        int y=bian[i].y;
        int a=bcj(x);
        int b=bcj(y);
        if(a==b)continue;
        fa[y]=x; 
        sum+=bian[i].w;
        num++;
        if(num==n-1)break;
    }
//  for(int i=1;i<=n;i++)
//      cout<<i<<"fa:"<<fa[i]<<endl;
    cout<<sum;
    return 0;
}

[方法2]prime最小生成树

基本思想：[加点]，从给定的根节点出发，每次找到其他点距离集合T最短的节点y(不是距离根节点最短的点),把y加入点中，如果一些点距离y比原来距离T更近，就用这些点距离y的长度更新距离T的长度

注意：dis[i]表示i到T集合(树)的最短距离，而不是到树中某个点的最短距离

[1]初始化：
    dis[自己]=0;
    dis[其他的点]=∞
    dis[自己的直接出边]=出边的权值
[2]需要做n-1次加点到T树中
    1.找到遍历其他的点i，找到dis[i]中最小的：y，并标记y已经用过
    2.把y加到T中，刷新dis[]

举例：

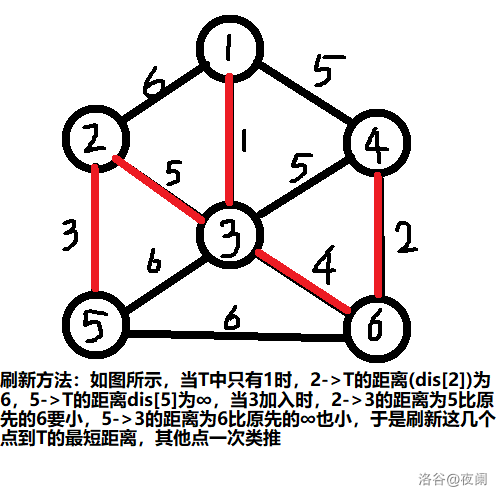
具体代码：(注释中的数据就是上图)

#include<iostream>
using namespace std;
/*
6   10
1  2  6
1  3   1
1  4   5
2  3  5
2  5  3
3  4  5
3  5  6
3  6  4
4  6  2
5  6  6
*/ 
int n,m,sum;
struct node{int to,w,next;};
node bian[50001];
int head[50001];
int cnt,dis[50001];
bool flag[50001];
void add(int x,int y,int w){
    cnt++;
    bian[cnt].w=w;
    bian[cnt].to=y;
    bian[cnt].next=head[x];
    head[x]=cnt;
}
void prime(int x){
    for(int i=1;i<=n;i++)
        dis[i]=987654321;   
    flag[x]=1;
    int y;
    for(int k=head[x];k;k=bian[k].next)
        dis[k]=bian[k].w;
    dis[x]=0;
    for(int i=1;i<=n-1;i++){
        int minn=987654321;
        for(int i=1;i<=n;i++){
            if(flag[i]==0&&dis[i]<minn){
                minn=dis[i];
                y=i;
            }
        }
        flag[y]=1;
        sum+=dis[y];
        dis[y]=0;
        for(int k=head[y];k;k=bian[k].next){
            if(bian[k].w<dis[bian[k].to]){
                dis[bian[k].to]=bian[k].w;
            }
        }
        cout<<"新加入的边：T->"<<y<<"权值："<<minn<<endl; 
    } 
    cout<<"最小生成树的权值为:"<<sum<<endl;
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        int x,y,w;
        cin>>x>>y>>w;
        add(x,y,w);
        add(y,x,w);
    }
    prime(1);
    return 0;
}

许金夫在2021-08-26 13:55:45追加了内容

日常打广告：

点击进入博客观看效果更优https://www.luogu.com.cn/blog/Luogu-Blog-Org/

点击进入博客观看效果更优https://www.luogu.com.cn/blog/Luogu-Blog-Org/

点击进入博客观看效果更优https://www.luogu.com.cn/blog/Luogu-Blog-Org/