字符串算法
字符串算法主要包括KMP,AC自动机,字典树.......
- 1 KMP算法
KMP:进行字符串的匹配
字符串算法的基**
在一个主串s中查找一个子串t,返回下标,否则-1
为了方便,所有的字符串下标从1开始(cin>>s+1),字符串用char[]表示
-暴力算法
用i遍历s,用j遍历t。最初ij指向t的第一个字符
ij一起向后挪,一个一个字符得比对,如果发现不同,ij回到t的开头,同时i++表示t向后一个一位
-核心函数
令s=ababcababa,t=ababa
核心思路:
用一个i指向s,用j指向t
一开始i,j所指的都是t的头,如果s[i]==t[j],i,j++
当s[i]!=t[j],也就是i,j=5时,我们会希望j不要回到头(会浪费)
我们发现ababa中前三个aba等于后三个
因为此时我们已经匹配了不少,已知1-4都是相同的,要是移动过后前面还是有一部分是相同的就会省时间
所以我们我们把ababa向后挪3格(j=3)
这样的话就是这样的:
ababcababa
ababa
可以看到此时j=3,i=5,但ij所指的位置一样
前面2个ab是相同的(省时间),但是s[i]还是不等于t[j]
因为j=3,前三个字符aba中相同的是a和a,所以我们把j更改为1
ababcababa
ababa
这次开头不一样,再往后挪一下
ababcababa
ababa
匹配成功在上面的过程中可以发现当j在快速变化的时候,数值很特殊(最大真前缀后缀相同的长度)
这个特殊的数组就是p[t]
-求数组p[t]
数组p[t]表示t[1-t]中所有满足t[1,k]==t[j-k+1,j]中k的最大值,也就是所有前缀==后缀中最长的那个的长度k
p[j]数组是我们在减少暴力算法中j的遍历次数
void pre(){//填p数组
p[1]=0;//初始化
int j=0;//要求的最大前缀后缀相同的长度
for(int i=1;i<m;i++){//自己和自己匹配
while(j>0&&b[j+1]!=b[i+1])//如果j不等于0代表正在向后匹配,如果发现不同,就后退
j=p[j];//后退
if(b[j+1]==b[i+1])j++;//自己和自己匹配,如果相同就增加
p[i+1]=j;//为了继续往后做
}
} -函数实现
因为求p[t]的过程就是t和自己匹配,而kmp主函数的过程就是s和t匹配,所以函数很相近,具体见完整代码
-完整代码
#include<bits/stdc++.h>
using namespace std;
int p[10010],n,m;
char s[10010],t[10010];
void pre(){
p[1]=0;//边界
int j=0;//要求的最大真前后缀长度
for(int i=1;i<m;i++){
while(j>0&&t[i+1]!=t[j+1])//连续前移直到不能退回前面
j=p[j];
if(t[i+1]==t[j+1])j++;
p[i+1]=j;
}
}
void kmp(){
int j=0;//这个j是指遍历t的下标
for(int i=1;i<n;i++){
while(j>0&&s[i+1]!=t[j+1])j=p[j];//如果匹配没成功就退回前面
if(s[i+1]==t[j+1])j++;
if(j==m){
cout<<i+1-j+1<<endl;//匹配成功,输出头的下标
j=p[j];//解可能不止一个,继续找
}
}
}
int main(){
cin>>s+1;//下标从1开始
cin>>t+1;
n=strlen(s+1);
m=strlen(t+1);
pre();kmp();
return 0;
}所以kmp十分的简介,我们可以把它背掉
许金夫在2022-03-20 22:44:37追加了内容
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
许金夫在2022-04-17 12:43:41追加了内容
更新啦:
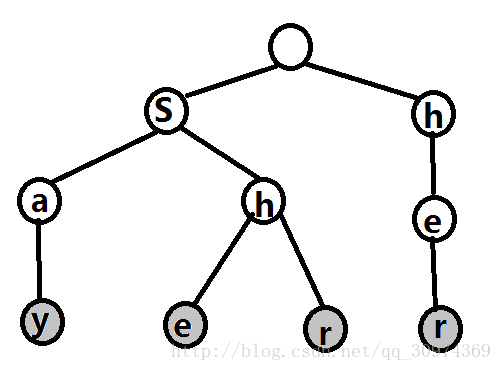
字典树
用字母表示的树,字母在边上,不在顶点上
利用公共前缀来节约内存
字典树是一个26叉树
题目中可以用来判断前缀(书P84)
思路:..................................
代码:
struct node{//trie结构
bool end;//这个点是否是一个字符串的结尾
int vis[30];//接下来一个节点的位置
}trie[10010];
int n,cnt;//cnt:点的下标
void build(string s){//插入s
int sp=0;//当前节点位置
int l=s.length();
for(int i=0;i<n;i++){
if(trie[sp].vis[s[i]]==0)//没有这个节点
trie[sp].vis[s[i]]==++cnt;//构建出这个节点
sp=cnt; //移到这个节点上
}
}WA自动机
kmp:单个字符串匹配单个字符串
ac自动机:一堆字符串匹配单个字符串(出现位置或出现次数)
1:构建一个trie树
代码见上
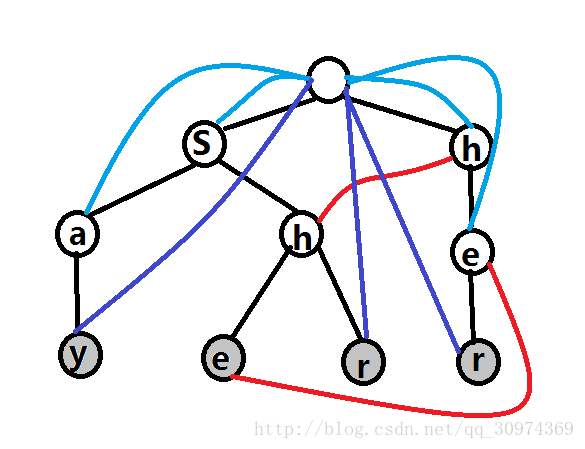
2:构建失配指针next[],类似kmp里的那个
- 一个节点的指针指向:沿着其父节点的失配指针,一直向上,直到找到拥有“当前这个字母的子节点”的节点,指针指向被找到的节点的子节点
- 第二层的所有指针指向根节点
- 底下的找不到也指向根节点
举两个例子:
s的儿子h节点的父节点在第二层,指向根节点,根节点有一个子节点也是h,所以s底下的h指向跟底下的h
s的孙子e节点的父节点h指向根的儿子h,那个h有一个儿子也是e,所以s的孙子e指向根的孙子e
类似kmp中的next代码需要使用BFS(用到队列),总代码在后面
3:匹配字符串
#include<bits/stdc++.h>
using namespace std;
struct node{
int fail;//失配指针
bool end;//字符串结尾标记
int vis[30];//接下来一个节点的位置
}trie[10010];//树
int n,cnt;//cnt:点下标
void build(string s){
int sp=0;//当前节点位置(根)
int l=s.length();
for(int i=0;i<l;i++){
if(trie[sp].vis[s[i]-'a']==0)
trie[sp].vis[s[i]-'a']=++cnt;
sp=cnt;
}
}
void faill(){//求fail
queue<int> q;
for(int i=0;i<26;i++){//预处理第二层的指针指向根节点
if(trie[0].vis[i]!=0){//如果存在这个节点
trie[0].fail=0;//指向根节点
q.push(trie[0].vis[i]);//把这个节点入队
}
}
while(!q.empty()){//队不空
int u=q.front();//出队首,开始bfs
q.pop();
for(int i=0;i<26;i++){//找u的所有子节点
if(trie[u].vis[i]!=0){
trie[trie[u].vis[i]].fail=trie[trie[u].fail].vis[i];
//找到拥有“当前这个字母的子节点”的节点,指针指向被找到的节点的子节点
q.push(trie[u].vis[i]);
}
else {
trie[u].vis[i]=trie[trie[u].fail].vis[i];
//当前节点的这个子节点指向当前节点fail指针的这个子节点
}
//这个if-else要画图
}
}
}
int check(string s){
int l=s.length();
int sp=0;//当前节点ac树上坐标
int ans=0;
for(int i=0;i<l;i++){//遍历
sp=trie[sp].vis[s[i]-'a'];//向下移动
for(int i=sp;i&&trie[i].end!=-1;i=trie[i].fail){
ans+=trie[i].end;
trie[i].end=-1;
}
}
return ans;
}
int main(){
return 0;
}许金夫在2022-04-17 12:44:43追加了内容
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
在博客内查看更优:https://www.luogu.com.cn/blog/Luogu-Blog-Org/zi-fu-chuan-suan-fa
在博客内查看更优:https://www.luogu.com.cn/blog/Luogu-Blog-Org/zi-fu-chuan-suan-fa
在博客内查看更优:https://www.luogu.com.cn/blog/Luogu-Blog-Org/zi-fu-chuan-suan-fa
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////