题目链接: 酷町堂:3074
3074 棋盘
经验值:1600 时间限制:1000毫秒 内存限制:256MB
全国 2017 NOIP 普及组试题
不许抄袭,一旦发现,直接清空经验!
题目描述 Deion
有一个m × m的棋盘,棋盘上每一个格子可能是红色、**或没有任何颜色的。你现在要从棋盘的最左上角走到棋盘的最右下角。
任何一个时刻,你所站在的位置必须是有颜色的(不能是无色的), 你只能向上、 下、左、 右四个方向前进。当你从一个格子走向另一个格子时,如果两个格子的颜色相同,那你不需要花费金币;如果不同,则你需要花费 1 个金币。
另外, 你可以花费 2 个金币施展魔法让下一个无色格子暂时变为你指定的颜色。但这个魔法不能连续使用, 而且这个魔法的持续时间很短,也就是说,如果你使用了这个魔法,走到了这个暂时有颜色的格子上,你就不能继续使用魔法; 只有当你离开这个位置,走到一个本来就有颜色的格子上的时候,你才能继续使用这个魔法,而当你离开了这个位置(施展魔法使得变为有颜色的格子)时,这个格子恢复为无色。
现在你要从棋盘的最左上角,走到棋盘的最右下角,求花费的最少金币是多少?
输入描述 Input Deion
数据的第一行包含两个正整数 m, n,以一个空格分开,分别代表棋盘的大小,棋盘上有颜色的格子的数量。
接下来的 n 行,每行三个正整数 x, y, c, 分别表示坐标为( x, y)的格子有颜色 c。
其中 c=1 代表**, c=0 代表红色。 相邻两个数之间用一个空格隔开。 棋盘左上角的坐标为( 1, 1),右下角的坐标为( m, m)。
棋盘上其余的格子都是无色。保证棋盘的左上角,也就是( 1, 1) 一定是有颜色的。
输出描述 Output Deion
输出一行,一个整数,表示花费的金币的最小值,如果无法到达,输出-1。
样例输入 Sample Input
输入样例1: 5 7 1 1 0 1 2 0 2 2 1 3 3 1 3 4 0 4 4 1 5 5 0 输入样例2: 5 5 1 1 0 1 2 0 2 2 1 3 3 1 5 5 0
样例输出 Sample Output
输出样例1: 8 输出样例2: -1
数据范围及提示 Data Size & Hint
数据规模与约定:
对于 30%的数据, 1 ≤ m ≤ 5, 1 ≤ n ≤ 10。
对于 60%的数据, 1 ≤ m ≤ 20, 1 ≤ n ≤ 200。
对于 100%的数据, 1 ≤ m ≤ 100, 1 ≤ n ≤ 1,000。
输入输出样例1说明:

从(1,1)开始,走到(1,2)不花费金币
从(1,2)向下走到(2,2)花费 1 枚金币
从(2,2)施展魔法,将(2,3)变为**,花费 2 枚金币
从(2,2)走到(2,3)不花费金币
从(2,3)走到(3,3)不花费金币
从(3,3)走到(3,4)花费 1 枚金币
从(3,4)走到(4,4)花费 1 枚金币
从(4,4)施展魔法,将(4,5)变为**,花费2 枚金币,
从(4,4)走到(4,5)不花费金币
从(4,5)走到(5,5)花费 1 枚金币
共花费 8 枚金币。
输入输出样例2说明:

从(1,1)走到(1,2),不花费金币
从(1,2)走到(2,2),花费1金币
施展魔法将(2,3)变为**,并从(2,2)走到(2,3)花费2金币
从(2,3)走到(3,3)不花费金币
从(3,3)只能施展魔法到达(3,2),(2,3),(3,4),(4,3)
而从以上四点均无法到达(5,5),故无法到达终点,输出-1
//CODE
//#pragma GCC optimize(3)
//#include <bits/stdc++.h>
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int m, n, ans;
int a[1005][1005];
int dir[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
bool used[1005][1005];
bool flag = true, check;
void dfs(int x, int y, int sum) {
if (sum >= ans) {
return ;
}
if (x == m && y == m) {
ans = min(ans, sum);
check = true;
return ;
}
for (int i = 0; i < 4; i ++) {
int nx = dir[i][0], ny = dir[i][1];
if (nx >= 1 && nx <= m && ny >= 1 && ny <= m && !used[nx][ny]) {
used[nx][ny] = true;
flag = true;
if (a[nx][ny] == a[x][y]) {
dfs(nx, ny, sum);
flag = true;
} else if (a[nx][ny] == 0 && a[x][y] == 1 || a[nx][ny] == 1 && a[x][y] == 0) {
dfs(nx, ny, sum + 1);
flag = true;
} else if (a[nx][ny] == -1 && flag) {
a[nx][ny] = a[x][y];
flag = false;
dfs(nx, ny, sum + 2);
flag = true;
a[nx][ny] = -1;
}
used[nx][ny] = false;
}
}
}
int main() {
// freopen ("题目名.in", "r", stdin);
// freopen ("题目名.out", "w", stdout);
memset(a, -1, sizeof(a));
cin >> m >> n;
for (int i = 1; i <= n; i ++) {
int u, v, f;
cin >> u >> v >> f;
a[u][v] = f;
}
used[1][1] = true;
dfs(1, 1, 0);
if (check) {
cout << ans;
} else {
cout << -1;
}
// fclose (stdin);
// fclose (stdout);
return 0;//好习惯!
}
至于本题的主流算法( dfs +记忆化优化),其实从最短路的角度上来讲是基于 dfs 实现的 SPFA (没错,就是那个**了又活了的SPFA),如果这一题数据范围扩大,并且做一些特殊构造,是可以被卡掉的。
另外,本蒟蒻不建议使用基于 dfs 实现的 SPFA ,因为这其实是最好卡掉了 SPFA 。
题意分析与转化
给你一个棋盘,有一些格子被染成了两种颜色。你可以从一个有颜色的格子走向另一个有颜色的格子,若两个格子颜色相同,则不付出代价,否则付出 11 点代价。
如果题目就到这里,相当于代价为 00 或者 11 的四个方向的走迷宫,可以使用双端队列 BFS 实现,时间复杂度O(m^2)O(m2)
另外, 你可以花费 22 个金币施展魔法让下一个无色格子暂时变为你指定的颜色。但这个魔法不能连续使用, 而且这个魔法的持续时间很短,也就是说,如果你使用了这个魔法,走到了这个暂时有颜色的格子上,你就不能继续使用魔法; 只有当你离开这个位置,走到一个本来就有颜色的格子上的时候,你才能继续使用这个魔法,而当你离开了这个位置(施展魔法使得变为有颜色的格子)时,这个格子恢复为无色。
如果就按照题意来直接搜索的话会比较麻烦(本蒟蒻当年就是这样写挂了的),但是我们可以稍微转化一下。
(注:下面的分析过程不妨只考虑一种颜色,因为颜色不同带来的代价的变化和魔法的转化没有太大关系)
我们现在站在一个施了魔法的格子上(称为 via ),我们上一步的格子称为 now ,下面我们思考下一步能走到的格子有哪些(称为 next )。
因为魔法不能连用,并且如果我们走回上一步的格子,结果一定不是最优的,所以我们可以选择的只有如下的情况:

其中蓝色的格子可能成为 next (前提,在未使用魔法的情况下这些格子本来有色)。
知道了 next 可能的决策集合,我们下面来看如何把魔法等价转换掉。
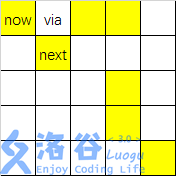
如图,可以将格子 via 施加魔法,从 now 走向 next ,实现了向右下方的转移。
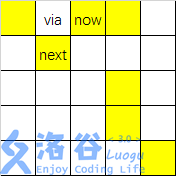
如图,可以将格子 via 施加魔法,从 now 走向 next ,实现了向左下方的转移。
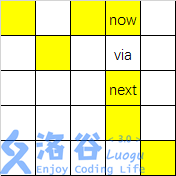
如图,可以将格子 via 施加魔法,从 now 走向 next ,实现了向下连跳22格的转移。
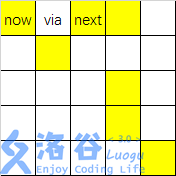
如图,可以将格子 via 施加魔法,从 now 走向 next ,实现了向右连22格的转移。
同理,我们也可以实现向左上方,向右上方,向上连跳22格,向左连跳22格的转移。
综上,我们得到使用魔法可以转移到的情况:

综合一下,我们可以得到如下结论:从 now 这个格子出发,使用或不使用魔法可以走到的有色格子的情况如下图:
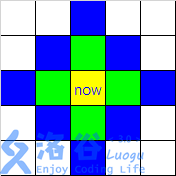
其中绿色格子因为使用魔法,不需要花费代价,蓝色的格子因为使用一次魔法,需要额外花费 22 点代价。(同样,这里不考虑格子实际颜色对代价的影响)
也许有同学会问了,如果出现下图中的这种情况呢?

显然从 now 出发先向右走后向下走是更优的,但是按照我们刚刚所述的方法,对 now 这个格子讨论,右下角的有色格子 B 会被认为要使用魔法,凭空多出了22点代价,我们刚刚的方法能得到最优解吗?
试问: now 右面的格子 A 是不是有色格子?
既然 A 是有色格子,那么我们也会对 A 讨论, now 可以不花费代价到达 A , A 又可以不花费代价到达 B ,因此 now 到 B 格子的代价最终会被 now->A->B 的路径取代,不会出现丢失最优解的情况。
这时我们发现一个问题:普通的 BFS 似乎实现不了这种答案更新,具体的分析与解法将在下文讲解。
现在我们先把颜色加上去:
- 与魔法无关的44种转移,同色代价不变,异色代价加 11 。
- 涉及魔法的88种转换,如果颜色相同,如图:

当格子 via 变成**的格子的时候,付出的代价最小,一共为22个代价。
如果颜色不同,如图:

当格子 via 变成**或者红色的时候,付出的代价都是一样的,一共为33个代价。
综上所述,我们将题目转化为如下:
你需要从(1,1)(1,1)走到(m,m)(m,m),你只能走在有颜色的格子中,并且使得你所花费的代价最小。
当你站在一个有颜色的格子上的时候,你可以进行如下22种操作:
- 向上、下、左、右前行。
- 向左上、左下、右上、右下、向上连跳22格、向下连跳22格、向左连跳22格、向右连跳22格前行。
如果你使用的是操作 22 ,你将额外付出 22 点代价。
在一次操作中,如果你这次操作的起点格子与终点格子颜色不同,你将付出11点代价。
完了吗?
显然没有!
如果(m,m)(m,m)没有颜色怎么办?
因为魔法不能连续使用,所以只可能从(m,m-1)(m,m−1),(m-1,m)(m−1,m)转移。
- 如果都没有颜色,就不可能到达(m,m)(m,m)。
- 如果任何一个有颜色,相当于(m,m)(m,m)变化为有颜色的那个格子的颜色,总代价为22。
- 如果22个都有颜色,转移总代价都是22,最后做一下比较就可以了。
算法分析
下面我们主要研究 BFS 的实现。
现在我们已经将题意转化为经典的走迷宫模型,解决的经典方法是 BFS ,但是又有所不同。每一次拓展的代价不一定相同,此时可能出现如下的情况: 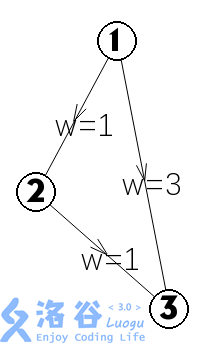
因为不满足三角形不等式,所以从实际来讲这里不应该画成三角形。但因为这张图简(wo)明(bi)直(jiao)观(lan),所以这张图就不重画了。
显然,最短路径应该是 1->2->3 ,而如果我们用一般的队列实现宽搜,就会得到错误的答案。
我们先思考一个问题:为什么经典的走迷宫模型可以直接普通队列 BFS ?
不难得出:在这样的 BFS 中,每一次扩展的代价都相等且为正数,后进入队列的状态一定不如先进入队列的状态优(先进入队列的状态的代价 \le≤ 后进入队列的状态的代价)。
基于这样的单调**,我们可以得出:第一次访问到某一个状态时,一定是这个状态的最优情况。
这是一个贪心思想。我们把这种思想应用到更具有普遍**的情况中:代价不一定相等。
现在我们有22种解决方法:
- 普通队列+迭代思想(已经**掉的
SPFA)
我们无法保证第一次访问到某一个状态的最优**,但我们可以将被优化的状态不断压入队列中,直到所有状态都是最优的。这种算法最坏情况下可以达到 O(n^2)O(n2) (n为状态种数),一般情况下为 O(n)O(n) 。
- 优先队列(
Dijkstra)
我们只要满足每一次都从状态队列中取出最小代价的状态,即可满足第一次访问最优**。优先队列可以实现这种操作。时间复杂度 O(n\log_2n)O(nlog2n) 。
有一种比较形象地解释,我们可以把 BFS 的棋盘看作图,即 Dijkstra 用来解决最短路。把这个图 “拎起来 ”,最初拎着起点,然后找当前最高的且没有被拎过的结点,作为下一次拎起来的结点,如此不断去拎,直到把终点结点拎起来,这样拎就可以找到起点和终点的最短距离。
注意,使用优先队列优化的 BFS 不能处理有负数代价的情况,反例如下:
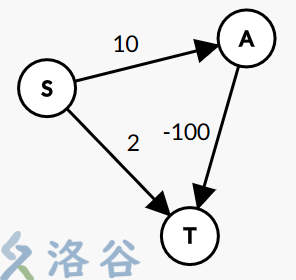
我们要从 S 走到 T ,第一步就可以找到所谓的最小代价22, A 虽然也在队列中,但是1010的代价比22大,因此不会被取出。
但实际上, S 走到 T 的最小代价是-90−90,路径为 S->A->T ,我们得到了错误的答案。
至此,我们成功跳出了命题人挖给我们的的思维陷阱,没有直接按照题意搜索,而是将题意转化,简化问题,大大降低了代码实现复杂度。(听说直接按照题意 dfs 会炸栈空间,虽然 NOIP 开大栈空间,但是你在跑大样例的时候看到程序报 RE 还找不到哪儿错了,对接下来做题的心态会有很大影响)
update on 2020.2.16. CSP-S 2019 的时候,我的几个同学因为不会开大栈空间 Day1T2 没法测大样例,丢分严重,且影响到 Day2 的发挥。







