问题标题: 洛谷：P1144 最短路计数

const int maxn=1000000+1,maxm=2000000+1,INF=0x7f7f7f7f,MOD=100003; vector<int>G[maxn];int dep[maxn];bool vis[maxn];int cnt[maxn]; int main(){ int N,M;scanf("%d%d",&N,&M); for(int i=1;i<=M;i++){ int x,y;scanf("%d%d",&x,&y); G[x].push_back(y); G[y].push_back(x); } queue<int>Q;dep[1]=0;vis[1]=1;Q.push(1);cnt[1]=1; while(!Q.empty()){ int x=Q.front();Q.pop(); for(int i=0;i<G[x].size();i++){ int t=G[x][i]; if(!vis[t]){vis[t]=1;dep[t]=dep[x]+1;Q.push(t);} if(dep[t]==dep[x]+1){cnt[t]=(cnt[t]+cnt[x])%MOD;} } } for(int i=1;i<=N;i++){ printf("%d\n",cnt[i]); } return 0;

这一道题实际上是一道很经典的搜索题，但是仍有很多人（包括我）被数据范围给吓到了，所以写了一个SPFA。

然而我翻了一下楼下各神犇的SPFA解法，发现了一个问题。由于此题的特殊性（每条边边权都是1），所以此题写SPFA其实可以当成一个广度优先搜索，不会有重复计数。然而，假如边有不同的边权，则对于如下图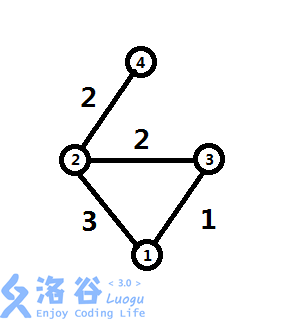：  从1出发，首先将2入队，再将3入队。此时，2节点的最短路条数为1。此时，1出队，2作为新的更新点，将4的最短路条数更新为1。然后，2出队，3作为出发点，更新2的最短路条数为2。此时，2又一次入队，将4的最短路条数更新为1+2=3。然而，易发现到4的最短路条数只有两条（1->2->4&1->3->2->4）。原因是有一条到2的最短路被重复计数了。因此，虽然在此题中没有必要，但是为了通用性，可以将SPFA的计数方式进行调整