问题标题: AC自动机讲解，大家都很好奇吧

0
1
已解决
刘瑾瑜
刘瑾瑜
新手天翼
新手天翼

要学AC自动机需要自备两个前置技能:KMP和trie树(其实个人感觉不会kmp也行,失配指针的概念并不难)

其中,KMP是用于一对一的字符串匹配,而trie虽然能用于多模式匹配,但是每次匹配失败都需要进行回溯,如果模式串很长的话会很浪费时间,所以AC自动机应运而生,如同Manacher一样,AC自动机利用某些操作阻止了模式串匹配阶段的回溯,将时间复杂度优化到了O ( n ) O(n)O(n)(n)为文本串长度

 

 

AC 自动机是 以 Trie 的结构为基础，结合 KMP 的思想 建立的自动机，用于解决多模式匹配等任务。

AC 自动机本质上是 Trie 上的自动机。

在阅读本文之前，请先阅读 KMP 和 Trie。

 

解释

简单来说，建立一个 AC 自动机有两个步骤：

 

  1. 基础的 Trie 结构：将所有的模式串构成一棵 Trie。
  2. KMP 的思想：对 Trie 树上所有的结点构造失配指针。

建立完毕后，就可以利用它进行多模式匹配。

 

字典树构建

AC 自动机在初始时会将若干个模式串插入到一个 Trie 里，然后在 Trie 上建立 AC 自动机。这个 Trie 就是普通的 Trie，按照 Trie 原本的建树方法建树即可。

需要注意的是，Trie 中的结点表示的是某个模式串的前缀。我们在后文也将其称作状态。一个结点表示一个状态，Trie 的边就是状态的转移。

形式化地说，对于若干个模式串 ，将它们构建一棵字典树后的所有状态的集合记作 。

 

失配指针

AC 自动机利用一个 fail 指针来辅助多模式串的匹配。

状态  的 fail 指针指向另一个状态 ，其中 ，且  是  的最长后缀（即在若干个后缀状态中取最长的一个作为 fail 指针）。

fail 指针与 KMP 中的 next 指针相比：

 

  1. 共同点：两者同样是在失配的时候用于跳转的指针。
  2. 不同点：next 指针求的是最长 Border（即最长的相同前后缀），而 fail 指针指向所有模式串的前缀中匹配当前状态的最长后缀。

因为 KMP 只对一个模式串做匹配，而 AC 自动机要对多个模式串做匹配。有可能 fail 指针指向的结点对应着另一个模式串，两者前缀不同。

总结下来，AC 自动机的失配指针指向当前状态的最长后缀状态。

注意：AC 自动机在做匹配时，同一位上可匹配多个模式串。

 

构建指针

下面介绍构建 fail 指针的 基础思想：

构建 fail 指针，可以参考 KMP 中构造 Next 指针的思想。

考虑字典树中当前的结点 ， 的父结点是 ， 通过字符 c 的边指向 ，即 。假设深度小于  的所有结点的 fail 指针都已求得。

 

  1. 如果  存在：则让 u 的 fail 指针指向 。相当于在  和  后面加一个字符 c，分别对应  和 。
  2. 如果  不存在：那么我们继续找到 。重复 1 的判断过程，一直跳 fail 指针直到根结点。
  3. 如果依然不存在，就让 fail 指针指向根结点。

如此即完成了  的构建。

 

例子

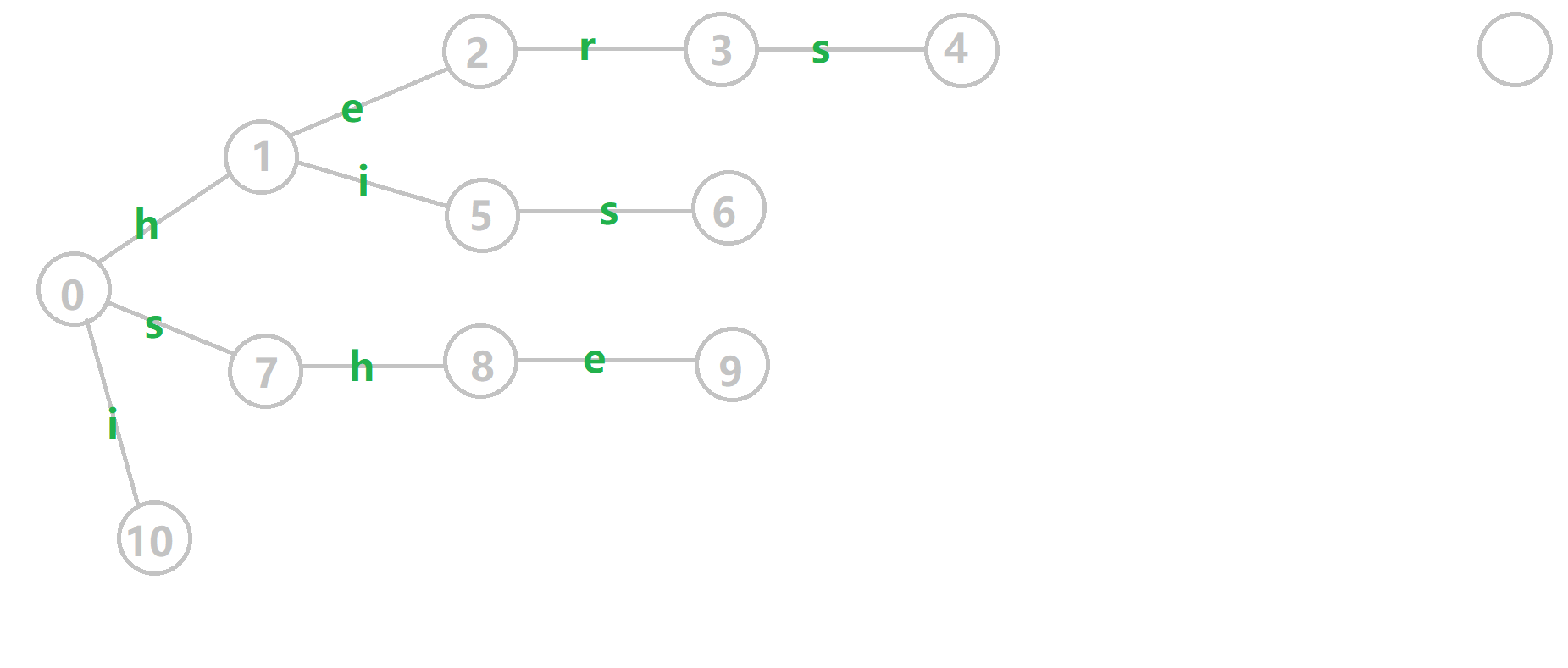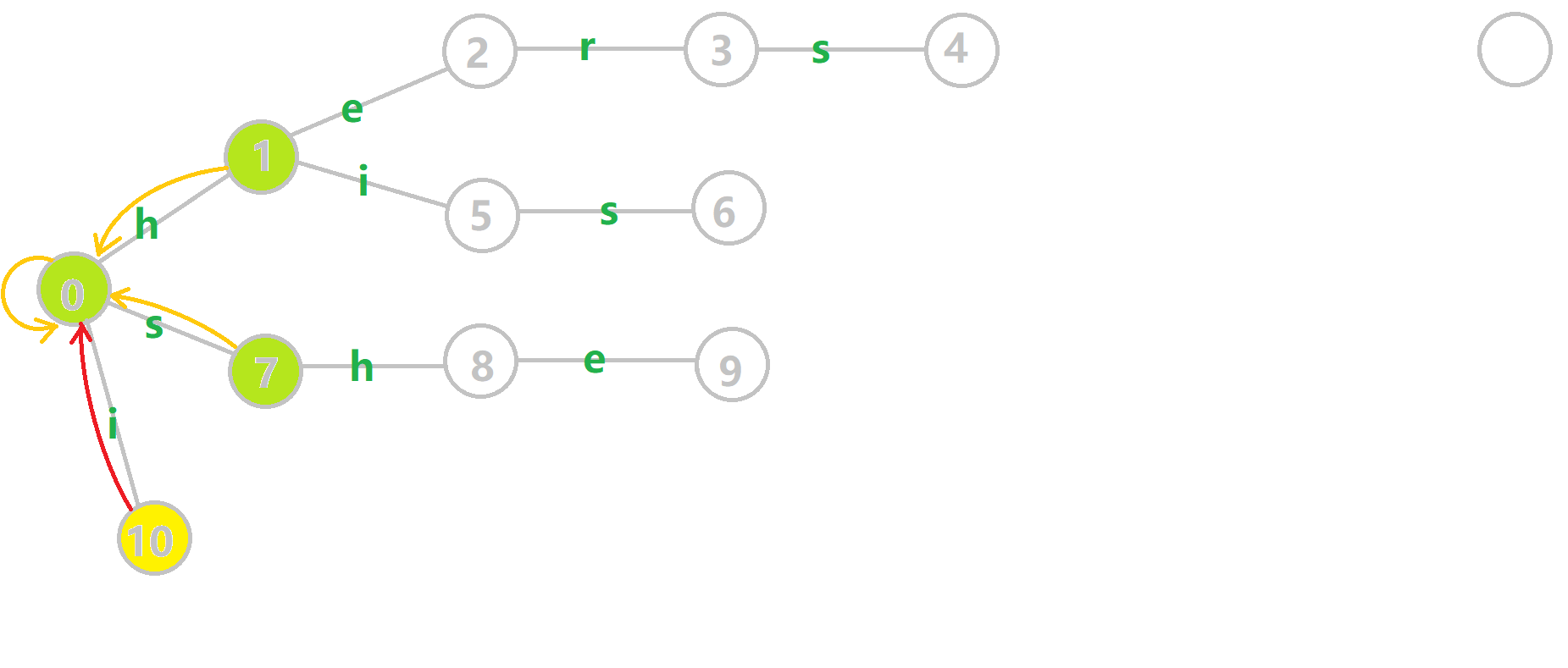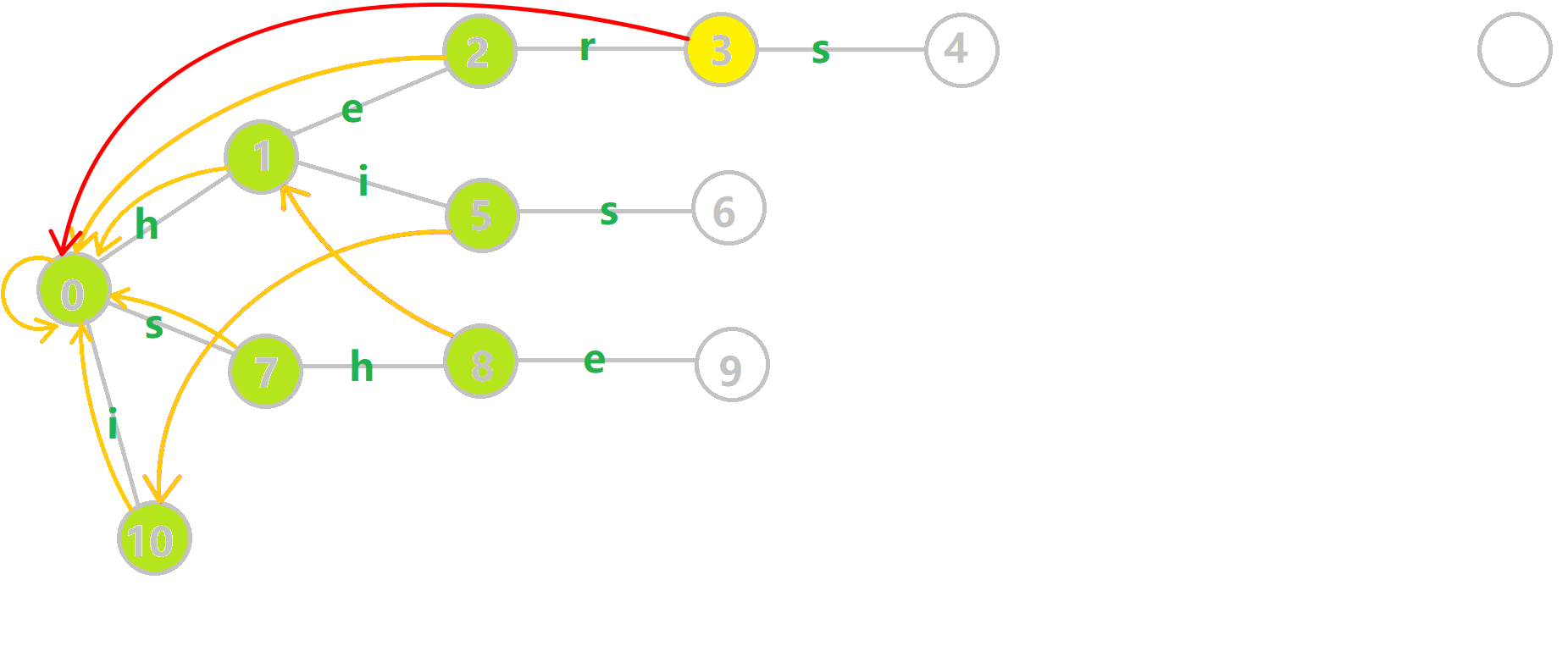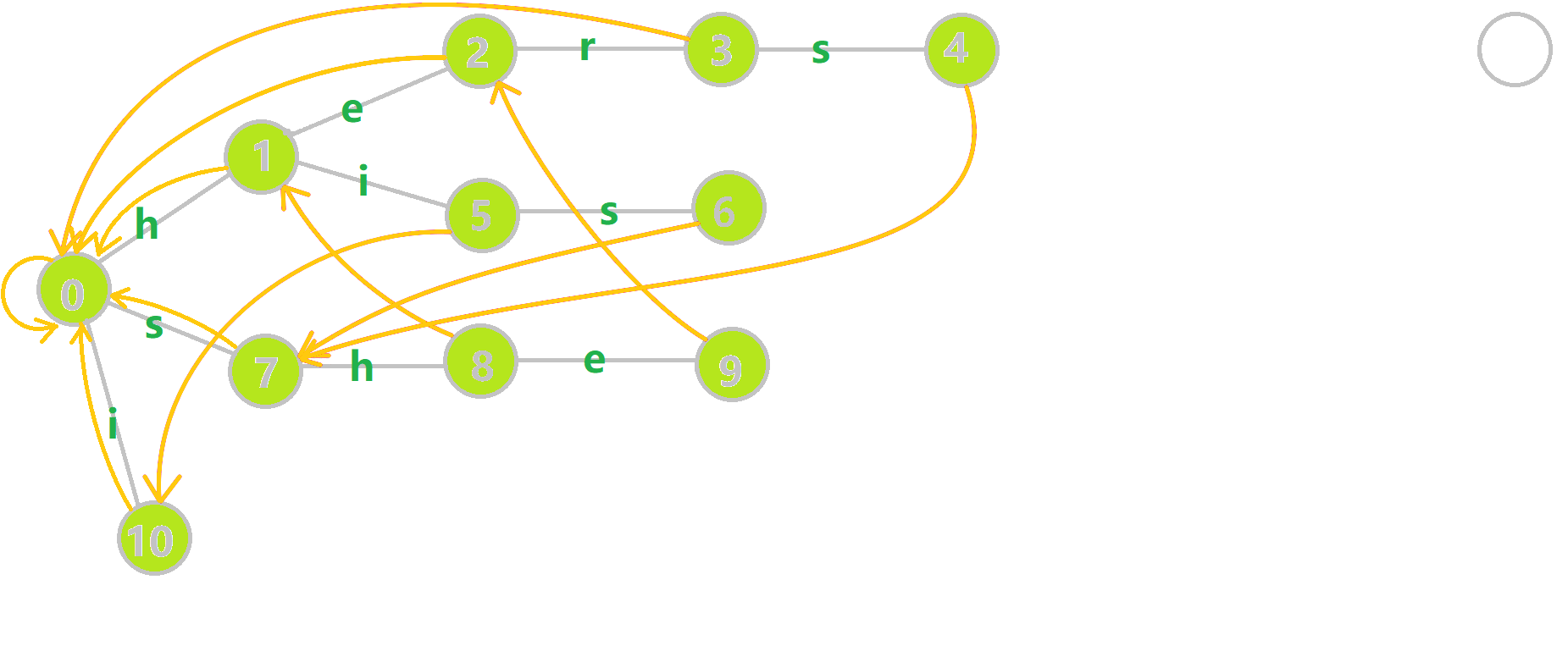
下面将使用若干张 GIF 动图来演示对字符串 i he his she hers 组成的字典树构建 fail 指针的过程：

 

  1. 黄色结点：当前的结点 。
  2. 绿色结点：表示已经 BFS 遍历完毕的结点，
  3. 橙色的边：fail 指针。
  4. 红色的边：当前求出的 fail 指针。

AC_automation_gif_b_3.gif

我们重点分析结点 6 的 fail 指针构建：

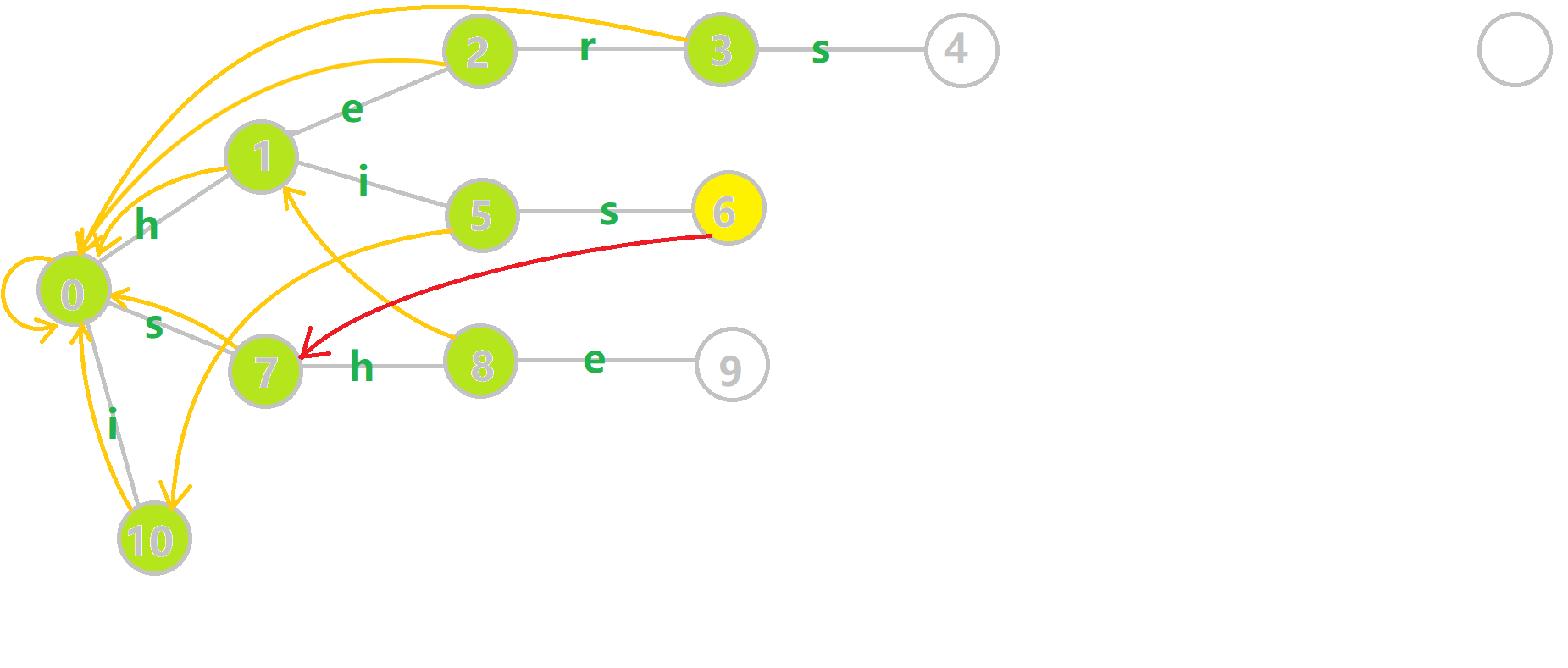
AC_automation_6_9.png

找到 6 的父结点 5，。然而 10 结点没有字母 s 连出的边；继续跳到 10 的 fail 指针，。发现 0 结点有字母 s 连出的边，指向 7 结点；所以 。

下图展示了构建完毕的状态：

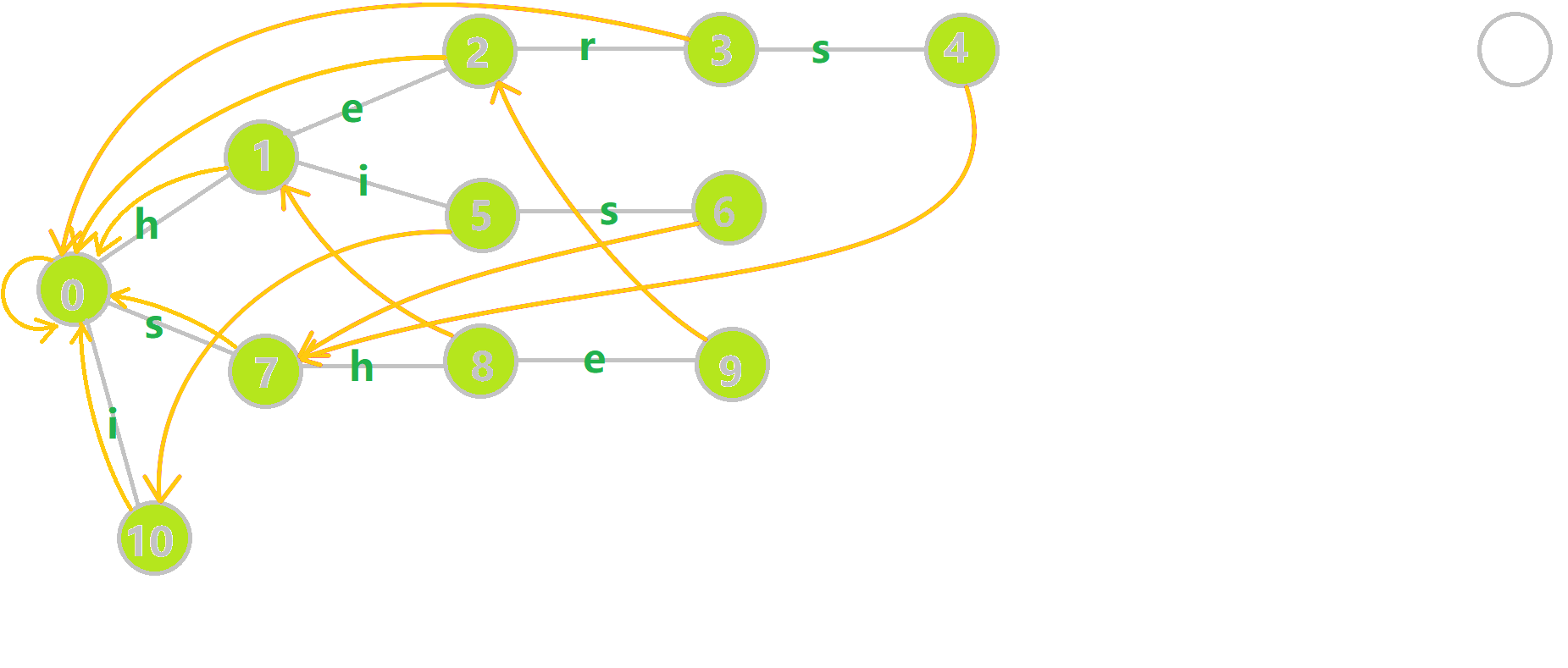
finish

 

字典树与字典图

关注构建函数 build()，该函数的目标有两个，一个是构建 fail 指针，一个是构建自动机。参数如下：

 

  1. tr[u,c]：有两种理解方式。我们可以简单理解为字典树上的一条边，即 ；也可以理解为从状态（结点） 后加一个字符 c 到达的状态（结点），即一个状态转移函数 。为了方便，下文中我们将用第二种理解方式。
  2. 队列 q：用于 BFS 遍历字典树。
  3. fail[u]：结点  的 fail 指针。

实现

C++

Python

void build() {
  for (int i = 0; i < 26; i++)
    if (tr[0][i]) q.push(tr[0][i]);
  while (q.size()) {
    int u = q.front();
    q.pop();
    for (int i = 0; i < 26; i++) {
      if (tr[u][i])
        fail[tr[u][i]] = tr[fail[u]][i], q.push(tr[u][i]);
      else
        tr[u][i] = tr[fail[u]][i];
    }
  }
}

解释

build 函数将结点按 BFS 顺序入队，依次求 fail 指针。这里的字典树根结点为 0，我们将根结点的子结点一一入队。若将根结点入队，则在第一次 BFS 的时候，会将根结点儿子的 fail 指针标记为本身。因此我们将根结点的儿子一一入队，而不是将根结点入队。

然后开始 BFS：每次取出队首的结点 u（ 在之前的 BFS 过程中已求得），然后遍历字符集（这里是 0-25，对应 a-z，即  的各个子节点）：

  1. 如果  存在，我们就将  的 fail 指针赋值为 。根据之前的描述，我们应该用 while 循环，不停的跳 fail 指针，判断是否存在字符 i 对应的结点，然后赋值，但此处通过特殊处理简化了这些代码。
  2. 否则，令  指向  的状态。

这里的处理是，通过 else 语句的代码修改字典树的结构，将不存在的字典树的状态链接到了失配指针的对应状态。在原字典树中，每一个结点代表一个字符串 ，是某个模式串的前缀。而在修改字典树结构后，尽管增加了许多转移关系，但结点（状态）所代表的字符串是不变的。

而  相当于是在  后添加一个字符 c 变成另一个状态 。如果  存在，说明存在一个模式串的前缀是 ，否则我们让  指向 。由于  对应的字符串是  的后缀，因此  对应的字符串也是  的后缀。

换言之在 Trie 上跳转的时侯，我们只会从  跳转到 ，相当于匹配了一个 ；但在 AC 自动机上跳转的时侯，我们会从  跳转到  的后缀，也就是说我们匹配一个字符 c，然后舍弃  的部分前缀。舍弃前缀显然是能匹配的。同时如果文本串能匹配 ，显然它也能匹配  的后缀，所以 fail 指针同样在舍弃前缀。所谓的 fail 指针其实就是  的一个后缀集合。

tr 数组还有另一种比较简单的理解方式：如果在位置  失配，我们会跳转到  的位置。注意这会导致我们可能沿着 fail 数组跳转多次才能来到下一个能匹配的位置。所以我们可以用 tr 数组直接记录记录下一个能匹配的位置，这样对程序的性能有一定的优化。

此处对字典树结构的修改，可以使得匹配转移更加完善。同时它将 fail 指针跳转的路径做了压缩，使得本来需要跳很多次 fail 指针变成跳一次。

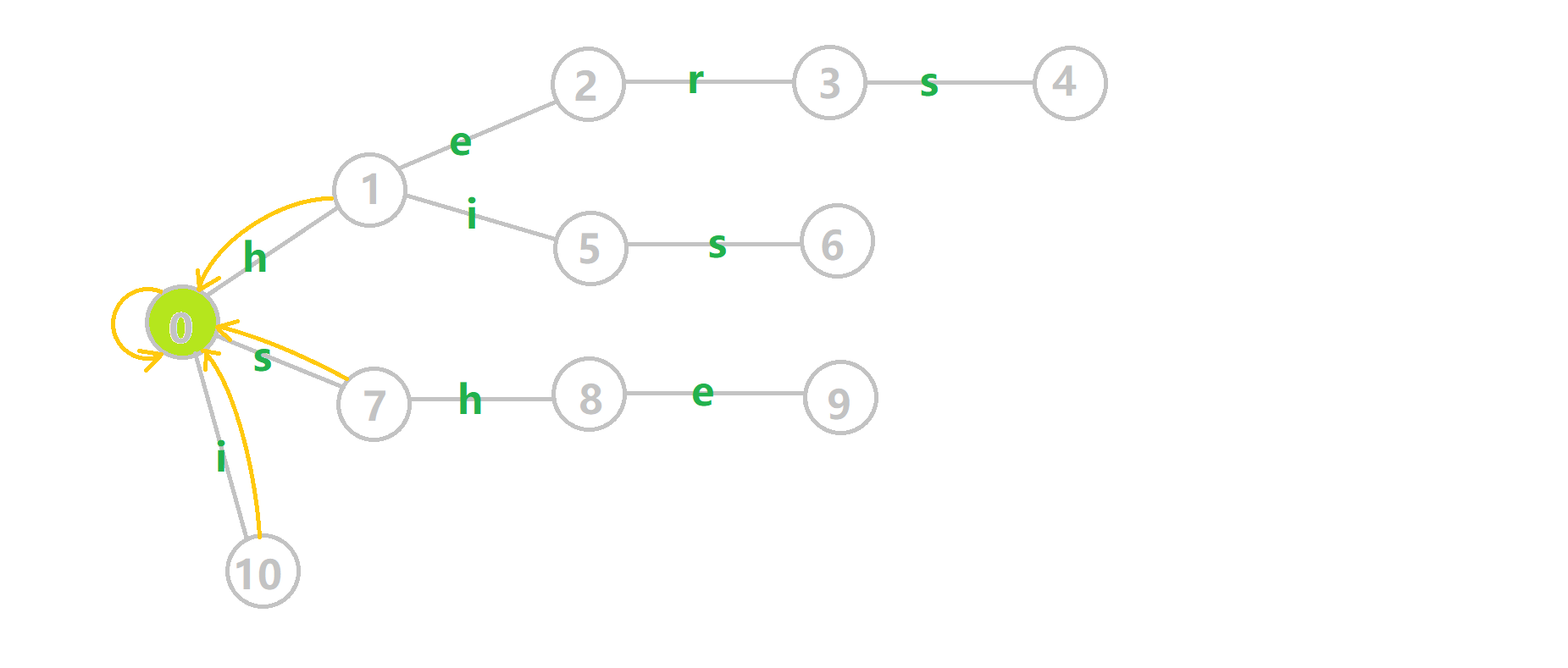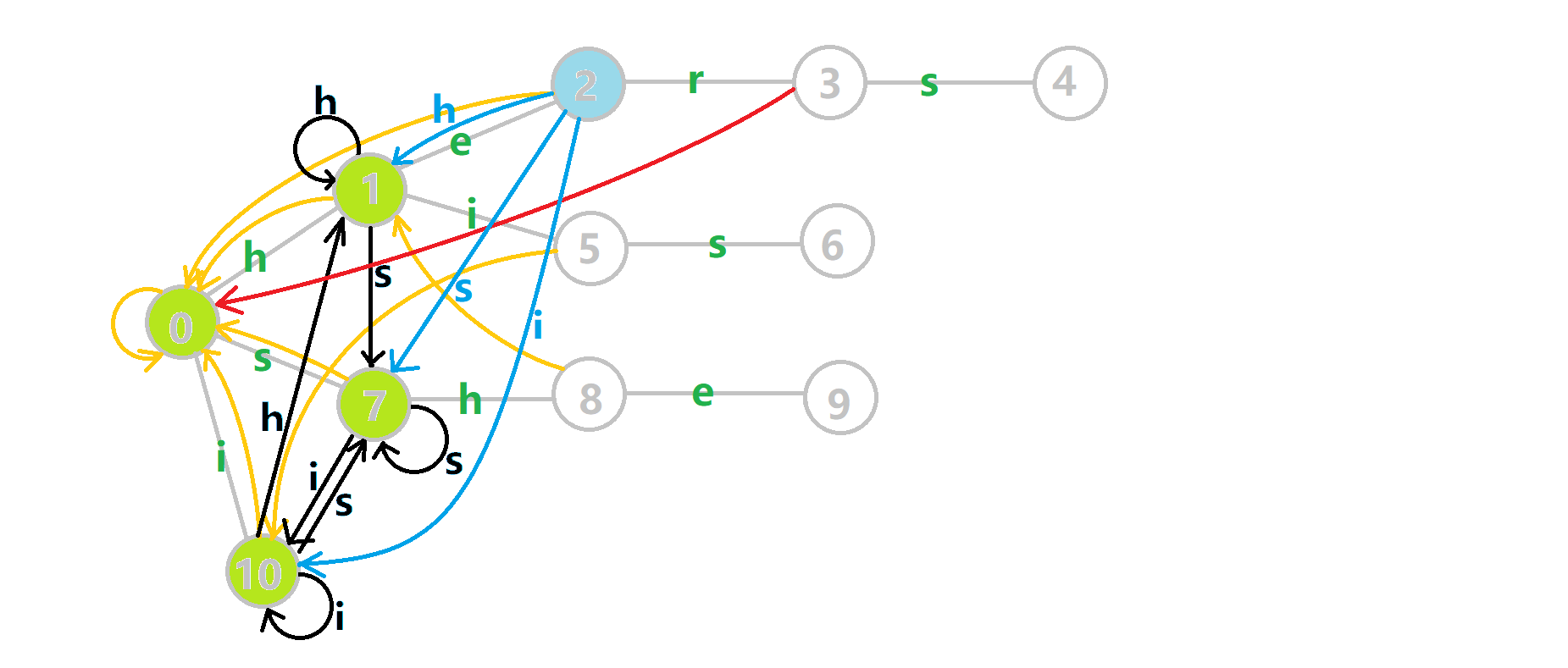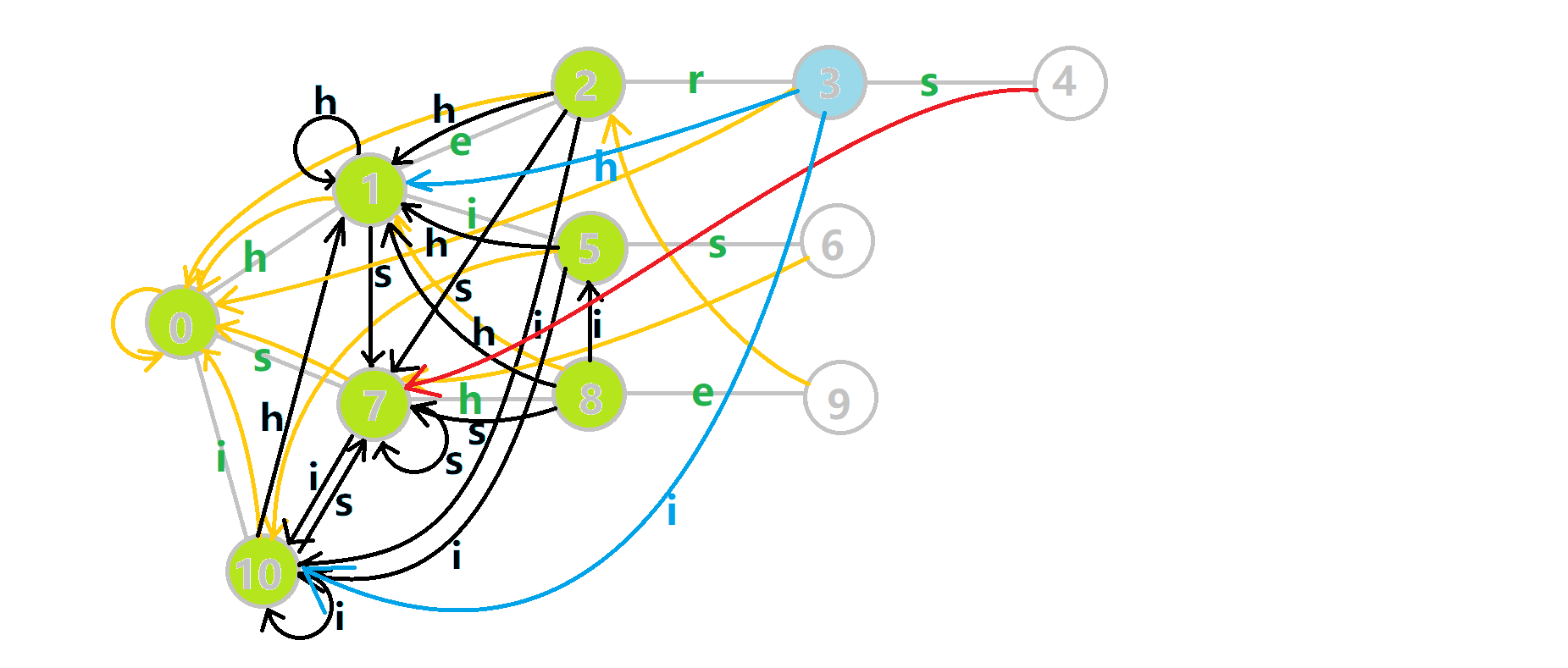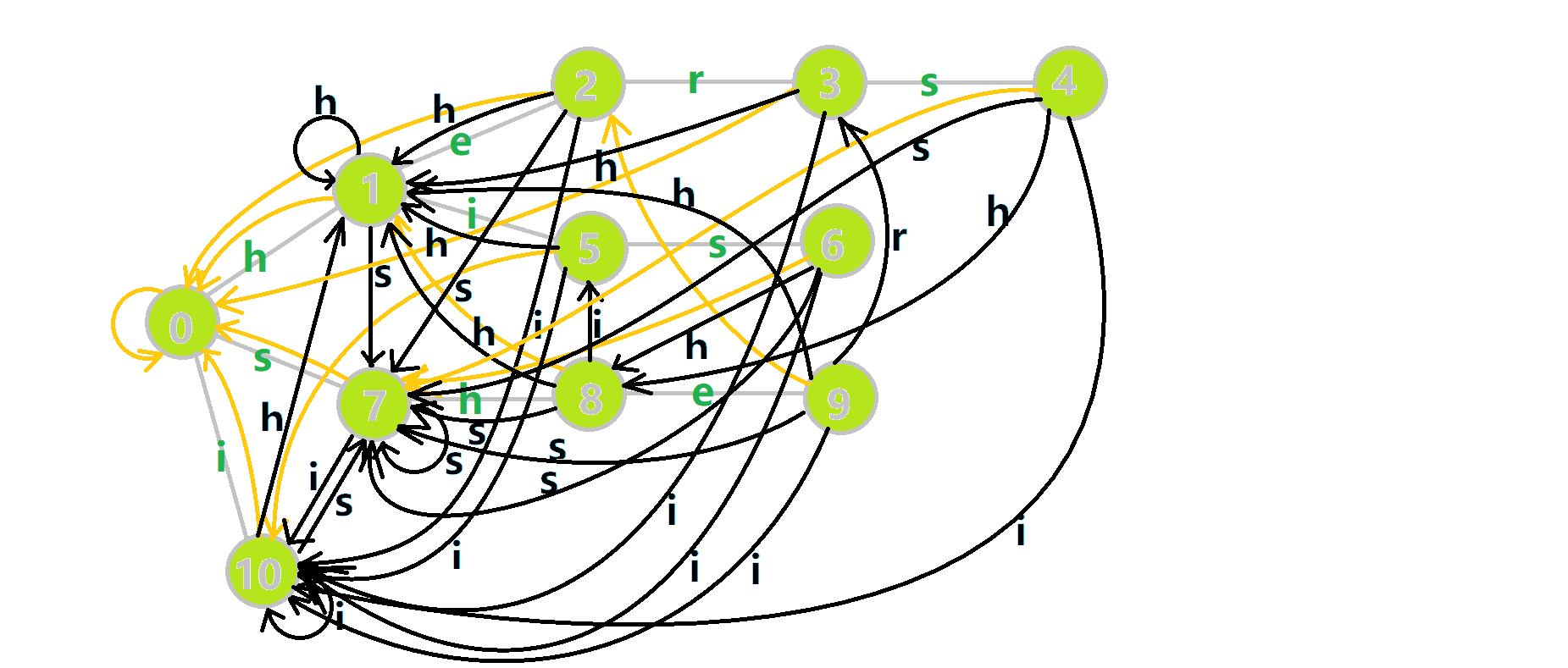
过程

这里依然用若干张 GIF 动图展示构建过程：

AC_automation_gif_b_pro3.gif

  1. 蓝色结点：BFS 遍历到的结点 u
  2. 蓝色的边：当前结点下，AC 自动机修改字典树结构连出的边。
  3. 黑色的边：AC 自动机修改字典树结构连出的边。
  4. 红色的边：当前结点求出的 fail 指针
  5. 黄色的边：fail 指针
  6. 灰色的边：字典树的边

可以发现，众多交错的黑色边将字典树变成了 字典图。图中省略了连向根结点的黑边（否则会更乱）。我们重点分析一下结点 5 遍历时的情况。我们求  的 fail 指针：

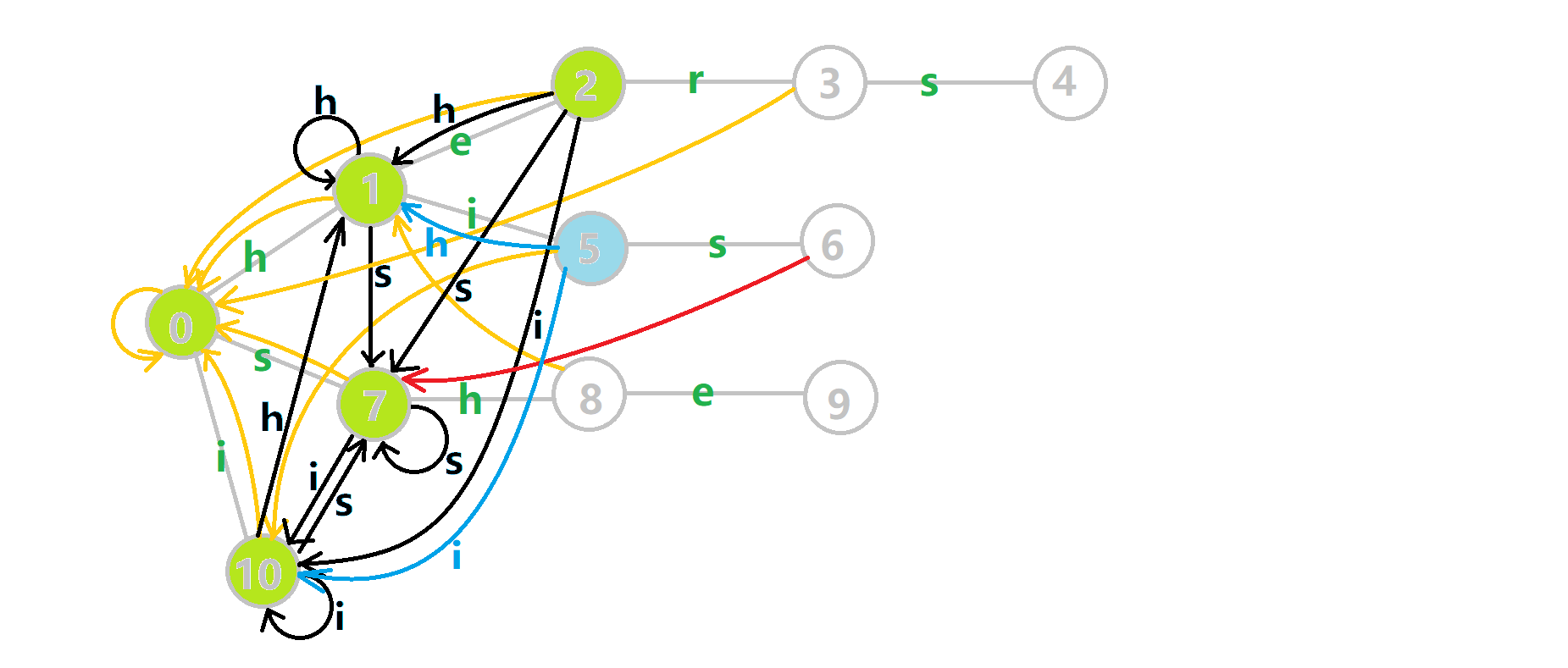
AC_automation_b_7.png

本来的策略是找 fail 指针，于是我们跳到  发现没有 s 连出的字典树的边，于是跳到 ，发现有 ，于是 ；但是有了黑边、蓝边，我们跳到  之后直接走  就走到  号结点了。

这就是 build 完成的两件事：构建 fail 指针和建立字典图。这个字典图也会在查询的时候起到关键作用。

多模式匹配

接下来分析匹配函数 query()：

实现

C++

Python

int query(char *t) {
  int u = 0, res = 0;
  for (int i = 1; t[i]; i++) {
    u = tr[u][t[i] - 'a'];  // 转移
    for (int j = u; j && e[j] != -1; j = fail[j]) {
      res += e[j], e[j] = -1;
    }
  }
  return res;
}

解释

这里  作为字典树上当前匹配到的结点，res 即返回的答案。循环遍历匹配串， 在字典树上跟踪当前字符。利用 fail 指针找出所有匹配的模式串，累加到答案中。然后清零。在上文中我们分析过，字典树的结构其实就是一个 trans 函数，而构建好这个函数后，在匹配字符串的过程中，我们会舍弃部分前缀达到最低限度的匹配。fail 指针则指向了更多的匹配状态。最后上一份图。对于刚才的自动机：

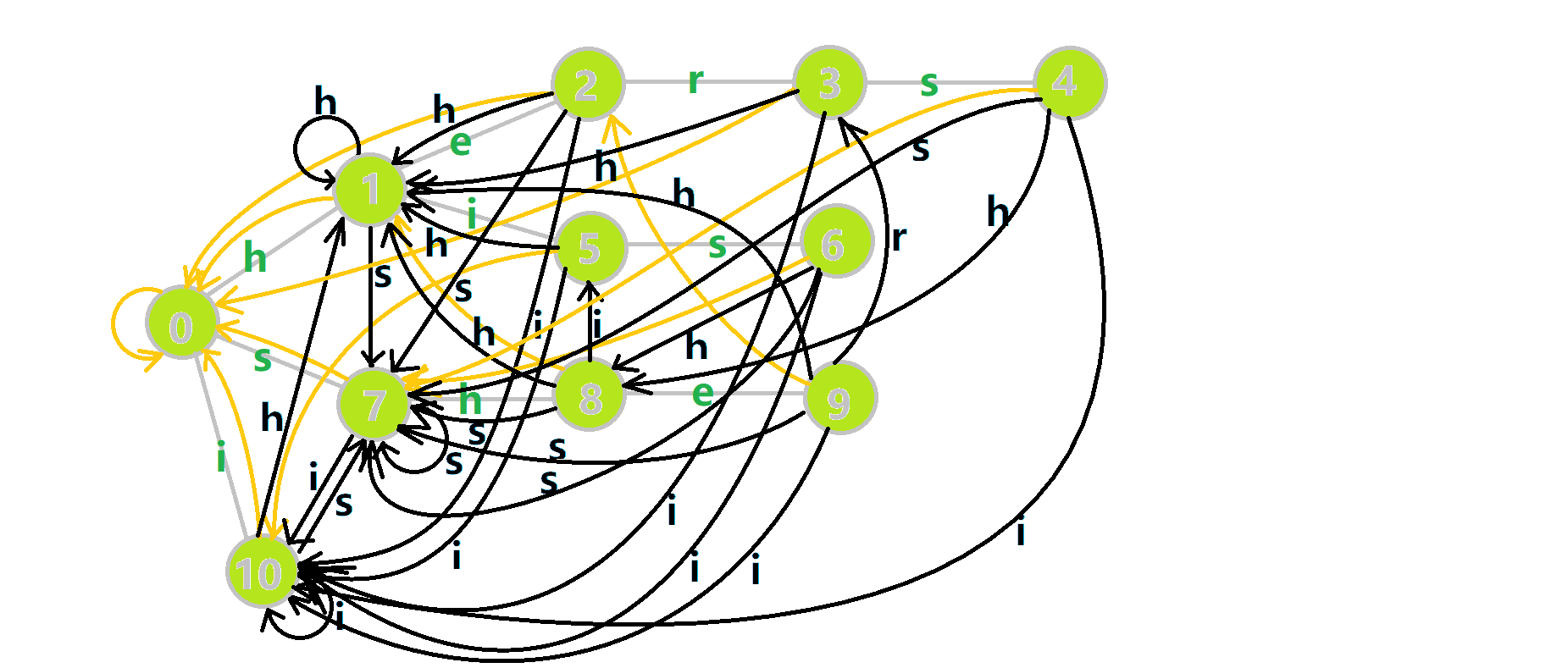
AC_automation_b_13.png

我们从根结点开始尝试匹配 ushersheishis，那么  的变化将是：

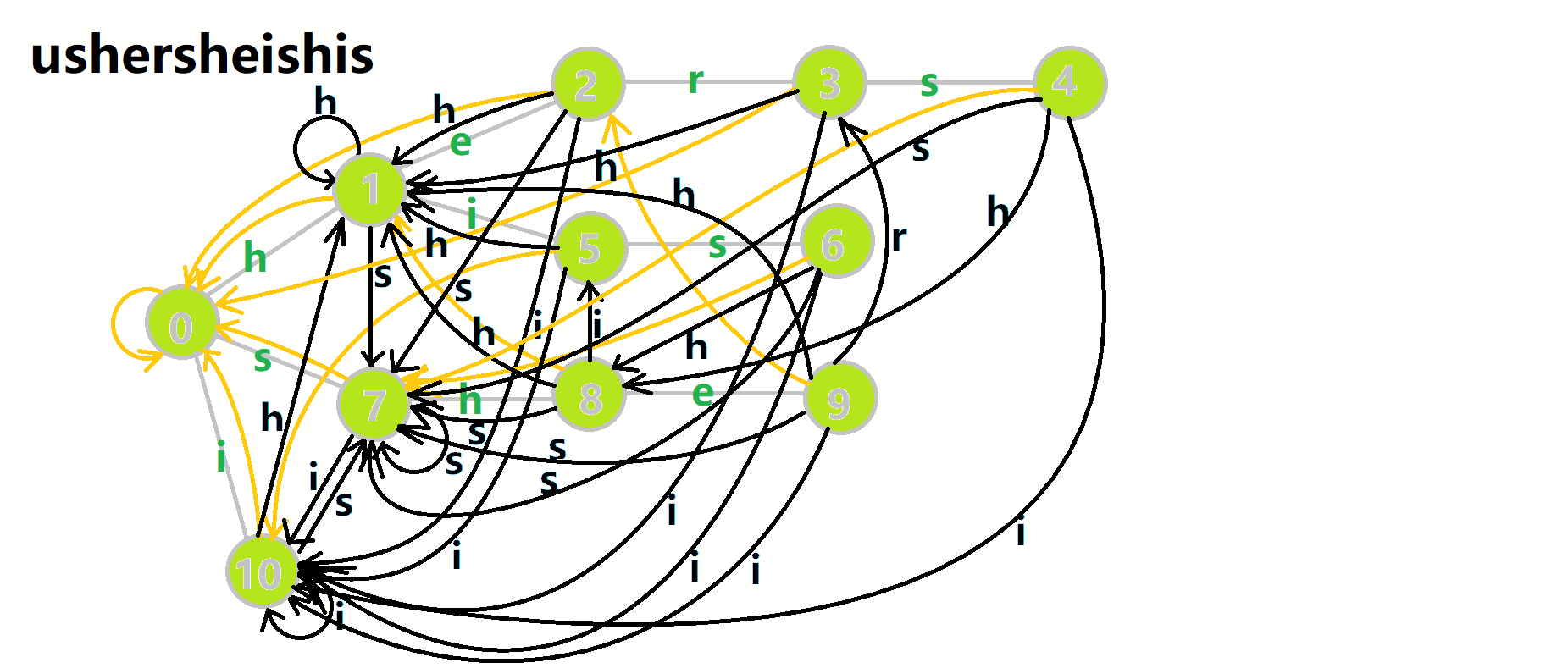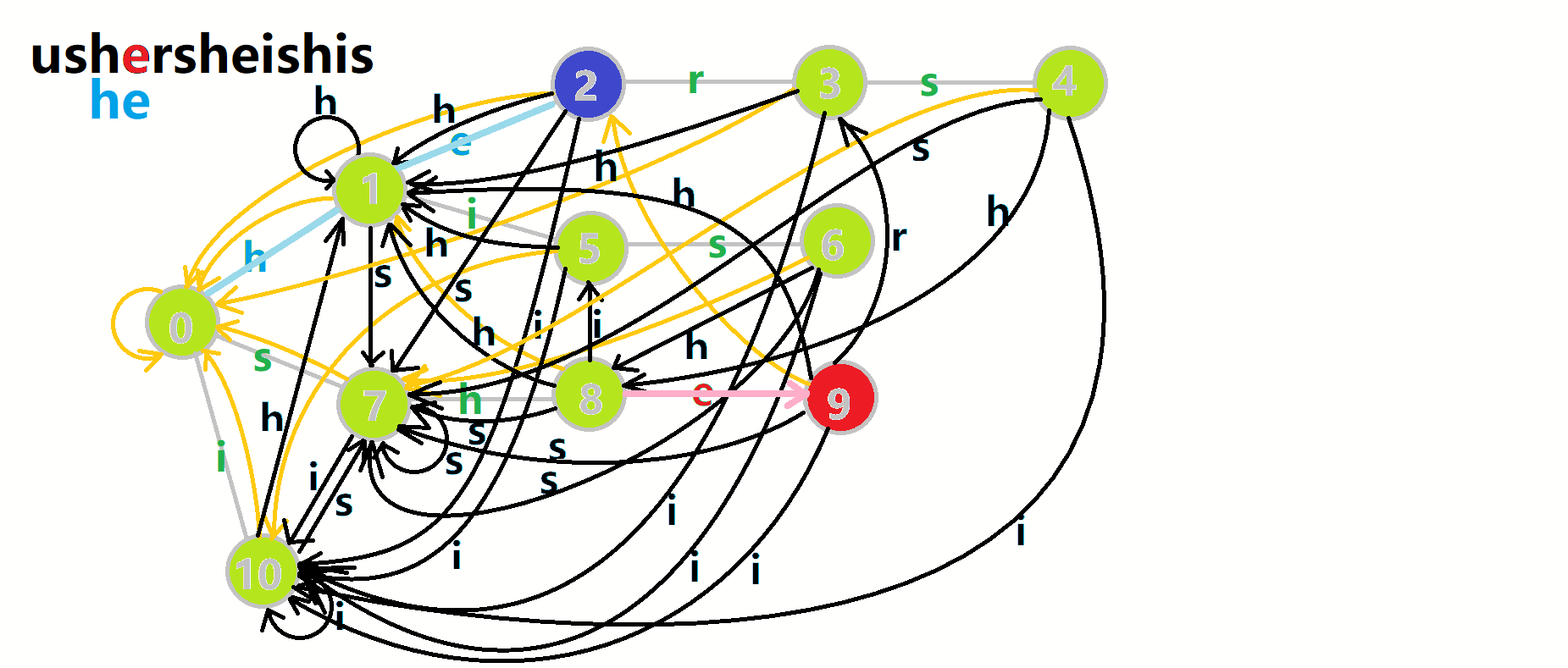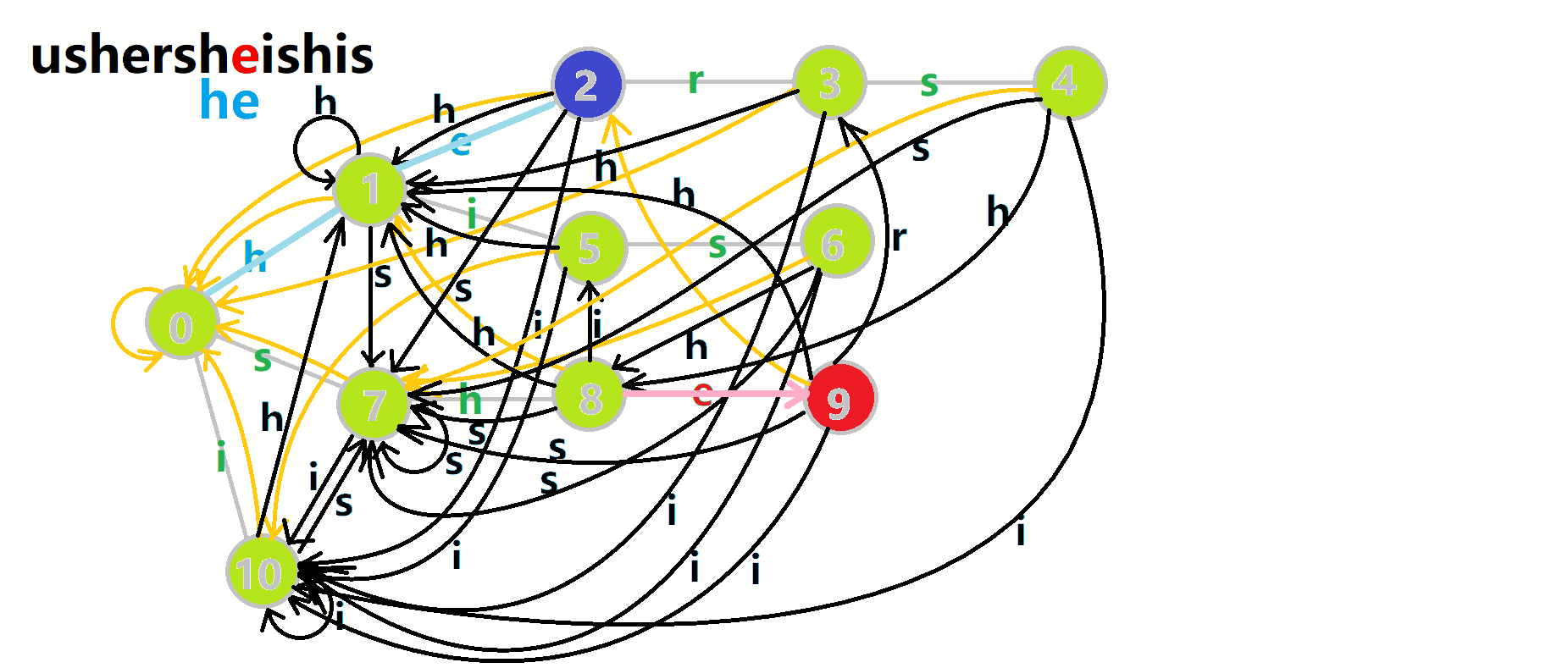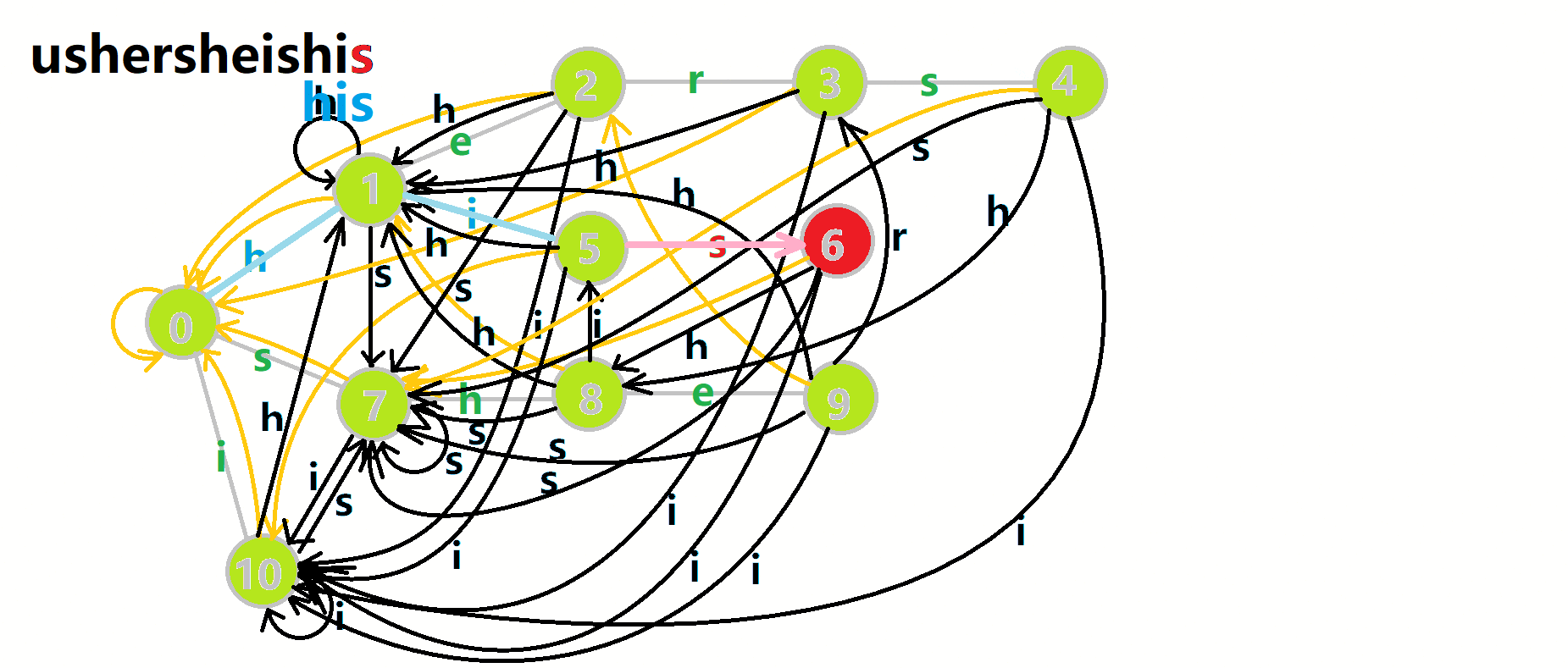
AC_automation_gif_c.gif

  1. 红色结点： 结点
  2. 粉色箭头： 在自动机上的跳转，
  3. 蓝色的边：成功匹配的模式串
  4. 蓝色结点：示跳 fail 指针时的结点（状态）。

效率优化

题目请参考洛谷 P5357【模板】AC 自动机（二次加强版）

因为我们的 AC 自动机中，每次匹配，会一直向 fail 边跳来找到所有的匹配，但是这样的效率较低，在某些题目中会超时。

那么我们如何优化呢？首先我们需要了解 fail 指针的一个性质：一个 AC 自动机中，如果只保留 fail 边，那么剩余的图一定是一棵树。

这是显然的，因为 fail 不会成环，且深度一定比现在低，所以得证。

而我们 AC 自动机的匹配就可以转化为在 fail 树上的链求和问题。

所以我们只需要优化一下这部分就可以了。

我们这里提供两种思路。

拓扑排序优化建图

观察到时间主要浪费在在每次都要跳 fail。如果我们可以预先记录，最后一并求和，那么效率就会优化。

于是我们按照 fail 树建图（注意不用真的建，只需要记录入度）：

建图

void getfail()  // 实际上也可以叫 build
{
  for (int i = 0; i < 26; i++) trie[0].son[i] = 1;
  q.push(1);
  trie[1].fail = 0;
  while (!q.empty()) {
    int u = q.front();
    q.pop();
    int Fail = trie[u].fail;
    for (int i = 0; i < 26; i++) {
      int v = trie[u].son[i];
      if (!v) {
        trie[u].son[i] = trie[Fail].son[i];
        continue;
      }
      trie[v].fail = trie[Fail].son[i];
      indeg[trie[Fail].son[i]]++;  // 修改点在这里，增加了入度记录
      q.push(v);
    }
  }
}

然后我们在查询的时候就可以只为找到节点的 ans 打上标记，在最后再用拓扑排序求出答案。

查询

void query(char *s) {
  int u = 1, len = strlen(s);
  for (int i = 0; i < len; i++) u = trie[u].son[s[i] - 'a'], trie[u].ans++;
}

void topu() {
  for (int i = 1; i <= cnt; i++)
    if (!indeg[i]) q.push(i);
  while (!q.empty()) {
    int fr = q.front();
    q.pop();
    vis[trie[fr].flag] = trie[fr].ans;
    int u = trie[fr].fail;
    trie[u].ans += trie[fr].ans;
    if (!(--indeg[u])) q.push(u);
  }
}

最后是主函数：

主函数

1
2
3
4
5
6
7

8

int main() {
  // do_something();
  scanf("%s", s);
  query(s);
  topu();
  for (int i = 1; i <= n; i++) cout << vis[rev[i]] << std::endl;
  // do_another_thing();
}

完整代码

Luogu P5357【模板】AC 自动机（二次加强版）


 
// Code by rickyxrc | https://www.luogu.com.cn/record/115706921
#include <bits/stdc++.h>
#define maxn 8000001
using namespace std;
char s[maxn];
int n, cnt, vis[maxn], rev[maxn], indeg[maxn], ans;

struct trie_node {
  int son[27];
  int fail;
  int flag;
  int ans;

  void init() {
    memset(son, 0, sizeof(son));
    fail = flag = 0;
  }
} trie[maxn];

queue<int> q;

void init() {
  for (int i = 0; i <= cnt; i++) trie[i].init();
  for (int i = 1; i <= n; i++) vis[i] = 0;
  cnt = 1;
  ans = 0;
}

void insert(char *s, int num) {
  int u = 1, len = strlen(s);
  for (int i = 0; i < len; i++) {
    int v = s[i] - 'a';
    if (!trie[u].son[v]) trie[u].son[v] = ++cnt;
    u = trie[u].son[v];
  }
  if (!trie[u].flag) trie[u].flag = num;
  rev[num] = trie[u].flag;
  return;
}

void getfail(void) {
  for (int i = 0; i < 26; i++) trie[0].son[i] = 1;
  q.push(1);
  trie[1].fail = 0;
  while (!q.empty()) {
    int u = q.front();
    q.pop();
    int Fail = trie[u].fail;
    for (int i = 0; i < 26; i++) {
      int v = trie[u].son[i];
      if (!v) {
        trie[u].son[i] = trie[Fail].son[i];
        continue;
      }
      trie[v].fail = trie[Fail].son[i];
      indeg[trie[Fail].son[i]]++;
      q.push(v);
    }
  }
}

void topu() {
  for (int i = 1; i <= cnt; i++)
    if (!indeg[i]) q.push(i);
  while (!q.empty()) {
    int fr = q.front();
    q.pop();
    vis[trie[fr].flag] = trie[fr].ans;
    int u = trie[fr].fail;
    trie[u].ans += trie[fr].ans;
    if (!(--indeg[u])) q.push(u);
  }
}

void query(char *s) {
  int u = 1, len = strlen(s);
  for (int i = 0; i < len; i++) u = trie[u].son[s[i] - 'a'], trie[u].ans++;
}

int main() {
  scanf("%d", &n);
  init();
  for (int i = 1; i <= n; i++) scanf("%s", s), insert(s, i);
  getfail();
  scanf("%s", s);
  query(s);
  topu();
  for (int i = 1; i <= n; i++) cout << vis[rev[i]] << std::endl;
  return 0;
}

子树求和

和拓扑排序的思路接近，我们预先将子树求和，询问时直接累加和值即可。

完整代码请见总结模板 3。

AC 自动机上 DP

这部分将以 P2292 [HNOI2004] L 语言 为例题讲解。

不难想到一个朴素的思路：建立 AC 自动机，在 AC 自动机上对于所有 fail 指针的子串转移，最后取最大值得到答案。

主要代码如下。若不熟悉代码中的类型定义，可以先看末尾的完整代码：

查询部分主要代码

void query(char *s) {
  int u = 1, len = strlen(s), l = 0;
  for (int i = 0; i < len; i++) {
    int v = s[i] - 'a';
    int k = trie[u].son[v];
    while (k > 1) {
      if (trie[k].flag && (dp[i - trie[k].len] || i - trie[k].len == -1))
        dp[i] = dp[i - trie[k].len] + trie[k].len;
      k = trie[k].fail;
    }
    u = trie[u].son[v];
  }
}

主函数里取 max 即可。

 

for (int i = 0, e = strlen(T); i < e; i++) mx = std::max(mx, dp[i]);

但是这样的思路复杂度不是线性（因为要跳每个节点的 fail），会在第二个子任务中超时，所以我们需要进行优化。

我们再看看题目的特殊性质，我们发现所有单词的长度只有 ，所以可以想到状态压缩优化。

我们发现，目前的时间瓶颈主要在跳 fail 这一步，如果我们可以将这一步优化到 ，就可以保证整个问题在严格线性的时间内被解出。

我们可以将前  位字母中，可能的子串长度存下来，并压缩到状态中，存在每个子节点中。

那么我们在 buildfail 的时候就可以这么写：

构建 fail 指针

void getfail(void) {
  for (int i = 0; i < 26; i++) trie[0].son[i] = 1;
  q.push(1);
  trie[1].fail = 0;
  while (!q.empty()) {
    int u = q.front();
    q.pop();
    int Fail = trie[u].fail;
    // 对状态的更新在这里
    trie[u].stat = trie[Fail].stat;
    if (trie[u].flag) trie[u].stat |= 1 << trie[u].depth;
    for (int i = 0; i < 26; i++) {
      int v = trie[u].son[i];
      if (!v)
        trie[u].son[i] = trie[Fail].son[i];
      else {
        trie[v].depth = trie[u].depth + 1;
        trie[v].fail = trie[Fail].son[i];
        q.push(v);
      }
    }
  }
}

然后查询时就可以去掉跳 fail 的循环，将代码简化如下：

查询

int query(char *s) {
  int u = 1, len = strlen(s), mx = 0;
  unsigned st = 1;
  for (int i = 0; i < len; i++) {
    int v = s[i] - 'a';
    u = trie[u].son[v];
    // 因为往下跳了一位每一位的长度都+1
    st <<= 1;
    // 这里的 & 值是状压 dp 的使用，代表两个长度集的交非空
    if (trie[u].stat & st) st |= 1, mx = i + 1;
  }
  return mx;
}

我们的 trie[u].stat 维护的是从 u 节点开始，整条 fail 链上的长度集（因为长度集小于 32 所以不影响），而 st 则维护的是查询字符串走到现在，前 32 位（因为状态压缩自然溢出）的长度集。

& 值不为 0，则代表两个长度集的交集非空，我们此时就找到了一个匹配。

完整代码

P2292 [HNOI2004] L 语言

// Code by rickyxrc | https://www.luogu.com.cn/record/115806238
#include <stdio.h>
#include <string.h>

#include <queue>
#define maxn 3000001
char T[maxn];
int n, cnt, vis[maxn], ans, m, dp[maxn];

struct trie_node {
  int son[26];
  int fail, flag, depth;
  unsigned stat;

  void init() {
    memset(son, 0, sizeof(son));
    fail = flag = depth = 0;
  }
} trie[maxn];

std::queue<int> q;

void init() {
  for (int i = 0; i <= cnt; i++) trie[i].init();
  for (int i = 1; i <= n; i++) vis[i] = 0;
  cnt = 1;
  ans = 0;
}

void insert(char *s, int num) {
  int u = 1, len = strlen(s);
  for (int i = 0; i < len; i++) {
    // trie[u].depth = i + 1;
    int v = s[i] - 'a';
    if (!trie[u].son[v]) trie[u].son[v] = ++cnt;
    u = trie[u].son[v];
  }
  trie[u].flag = num;
  // trie[u].stat = 1;
  // printf("set %d stat %d\n", u-1, 1);
  return;
}

void getfail(void) {
  for (int i = 0; i < 26; i++) trie[0].son[i] = 1;
  q.push(1);
  trie[1].fail = 0;
  while (!q.empty()) {
    int u = q.front();
    q.pop();
    int Fail = trie[u].fail;
    trie[u].stat = trie[Fail].stat;
    if (trie[u].flag) trie[u].stat |= 1 << trie[u].depth;
    for (int i = 0; i < 26; i++) {
      int v = trie[u].son[i];
      if (!v)
        trie[u].son[i] = trie[Fail].son[i];
      else {
        trie[v].depth = trie[u].depth + 1;
        trie[v].fail = trie[Fail].son[i];
        q.push(v);
      }
    }
  }
}

int query(char *s) {
  int u = 1, len = strlen(s), mx = 0;
  unsigned st = 1;
  for (int i = 0; i < len; i++) {
    int v = s[i] - 'a';
    u = trie[u].son[v];
    st <<= 1;
    if (trie[u].stat & st) st |= 1, mx = i + 1;
  }
  return mx;
}

int main() {
  scanf("%d%d", &n, &m);
  init();
  for (int i = 1; i <= n; i++) {
    scanf("%s", T);
    insert(T, i);
  }
  getfail();
  for (int i = 1; i <= m; i++) {
    scanf("%s", T);
    printf("%d\n", query(T));
  }
}

总结

时间复杂度：定义  是模板串的长度， 是文本串的长度， 是字符集的大小（常数，一般为 26）。如果连了 trie 图，时间复杂度就是 ，其中  是 AC 自动机中结点的数目，并且最大可以达到 。如果不连 trie 图，并且在构建 fail 指针的时候避免遍历到空儿子，时间复杂度就是 。

模板 1

Luogu P3808【模板】AC 自动机（简单版）

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 6;
int n;

namespace AC {
int tr[N][26], tot;
int e[N], fail[N];

void insert(char *s) {
  int u = 0;
  for (int i = 1; s[i]; i++) {
    if (!tr[u][s[i] - 'a']) tr[u][s[i] - 'a'] = ++tot;  // 如果没有则插入新节点
    u = tr[u][s[i] - 'a'];                              // 搜索下一个节点
  }
  e[u]++;  // 尾为节点 u 的串的个数
}

queue<int> q;

void build() {
  for (int i = 0; i < 26; i++)
    if (tr[0][i]) q.push(tr[0][i]);
  while (q.size()) {
    int u = q.front();
    q.pop();
    for (int i = 0; i < 26; i++) {
      if (tr[u][i]) {
        fail[tr[u][i]] =
            tr[fail[u]][i];  // fail数组：同一字符可以匹配的其他位置
        q.push(tr[u][i]);
      } else
        tr[u][i] = tr[fail[u]][i];
    }
  }
}

int query(char *t) {
  int u = 0, res = 0;
  for (int i = 1; t[i]; i++) {
    u = tr[u][t[i] - 'a'];  // 转移
    for (int j = u; j && e[j] != -1; j = fail[j]) {
      res += e[j], e[j] = -1;
    }
  }
  return res;
}
}  // namespace AC

char s[N];

int main() {
  scanf("%d", &n);
  for (int i = 1; i <= n; i++) scanf("%s", s + 1), AC::insert(s);
  scanf("%s", s + 1);
  AC::build();
  printf("%d", AC::query(s));
  return 0;
}

模板 2

Luogu P3796【模板】AC 自动机（加强版）

#include <bits/stdc++.h>
using namespace std;
const int N = 156, L = 1e6 + 6;

namespace AC {
const int SZ = N * 80;
int tot, tr[SZ][26];
int fail[SZ], idx[SZ], val[SZ];
int cnt[N];  // 记录第 i 个字符串的出现次数

void init() {
  memset(fail, 0, sizeof(fail));
  memset(tr, 0, sizeof(tr));
  memset(val, 0, sizeof(val));
  memset(cnt, 0, sizeof(cnt));
  memset(idx, 0, sizeof(idx));
  tot = 0;
}

void insert(char *s, int id) {  // id 表示原始字符串的编号
  int u = 0;
  for (int i = 1; s[i]; i++) {
    if (!tr[u][s[i] - 'a']) tr[u][s[i] - 'a'] = ++tot;
    u = tr[u][s[i] - 'a'];  // 转移
  }
  idx[u] = id;  // 以 u 为结尾的字符串编号为 idx[u]
}

queue<int> q;

void build() {
  for (int i = 0; i < 26; i++)
    if (tr[0][i]) q.push(tr[0][i]);
  while (q.size()) {
    int u = q.front();
    q.pop();
    for (int i = 0; i < 26; i++) {
      if (tr[u][i]) {
        fail[tr[u][i]] =
            tr[fail[u]][i];  // fail数组：同一字符可以匹配的其他位置
        q.push(tr[u][i]);
      } else
        tr[u][i] = tr[fail[u]][i];
    }
  }
}

int query(char *t) {  // 返回最大的出现次数
  int u = 0, res = 0;
  for (int i = 1; t[i]; i++) {
    u = tr[u][t[i] - 'a'];
    for (int j = u; j; j = fail[j]) val[j]++;
  }
  for (int i = 0; i <= tot; i++)
    if (idx[i]) res = max(res, val[i]), cnt[idx[i]] = val[i];
  return res;
}
}  // namespace AC

int n;
char s[N][100], t[L];

int main() {
  while (~scanf("%d", &n)) {
    if (n == 0) break;
    AC::init();  // 数组清零
    for (int i = 1; i <= n; i++)
      scanf("%s", s[i] + 1), AC::insert(s[i], i);  // 需要记录该字符串的序号
    AC::build();
    scanf("%s", t + 1);
    int x = AC::query(t);
    printf("%d\n", x);
    for (int i = 1; i <= n; i++)
      if (AC::cnt[i] == x) printf("%s\n", s[i] + 1);
  }
  return 0;
}

模版 3

Luogu P5357【模板】AC 自动机（二次加强版）

#include <deque>
#include <iostream>

void promote() {
  std::ios::sync_with_stdio(0);
  std::cin.tie(0);
  std::cout.tie(0);
  return;
}

typedef char chr;
typedef std::deque<int> dic;

const int maxN = 2e5;
const int maxS = 2e5;
const int maxT = 2e6;

int n;
chr s[maxS + 10];
chr t[maxT + 10];
int cnt[maxN + 10];

struct AhoCorasickAutomaton {
  struct Node {
    int son[30];
    int val;
    int fail;
    int head;
    dic index;
  } node[maxS + 10];

  struct Edge {
    int head;
    int next;
  } edge[maxS + 10];

  int root;
  int ncnt;
  int ecnt;

  void Insert(chr *str, int i) {
    int u = root;
    for (int i = 1; str[i]; i++) {
      if (node[u].son[str[i] - 'a' + 1] == 0)
        node[u].son[str[i] - 'a' + 1] = ++ncnt;
      u = node[u].son[str[i] - 'a' + 1];
    }
    node[u].index.push_back(i);
    return;
  }

  void Build() {
    dic q;
    for (int i = 1; i <= 26; i++)
      if (node[root].son[i]) q.push_back(node[root].son[i]);
    while (!q.empty()) {
      int u = q.front();
      q.pop_front();
      for (int i = 1; i <= 26; i++) {
        if (node[u].son[i]) {
          node[node[u].son[i]].fail = node[node[u].fail].son[i];
          q.push_back(node[u].son[i]);
        } else {
          node[u].son[i] = node[node[u].fail].son[i];
        }
      }
    }
    return;
  }

  void Query(chr *str) {
    int u = root;
    for (int i = 1; str[i]; i++) {
      u = node[u].son[str[i] - 'a' + 1];
      node[u].val++;
    }
    return;
  }

  void addEdge(int tail, int head) {
    ecnt++;
    edge[ecnt].head = head;
    edge[ecnt].next = node[tail].head;
    node[tail].head = ecnt;
    return;
  }

  void DFS(int u) {
    for (int e = node[u].head; e; e = edge[e].next) {
      int v = edge[e].head;
      DFS(v);
      node[u].val += node[v].val;
    }
    for (auto i : node[u].index) cnt[i] += node[u].val;
    return;
  }

  void FailTree() {
    for (int u = 1; u <= ncnt; u++) addEdge(node[u].fail, u);
    DFS(root);
    return;
  }
} ACM;

int main() {
  std::cin >> n;
  for (int i = 1; i <= n; i++) {
    std::cin >> (s + 1);
    ACM.Insert(s, i);
  }
  ACM.Build();
  std::cin >> (t + 1);
  ACM.Query(t);
  ACM.FailTree();
  for (int i = 1; i <= n; i++) std::cout << cnt[i] << '\n';
  return 0;
}

拓展

确定有限状态自动机

作为拓展延伸，文末我们简单介绍一下 自动机 与 KMP 自动机。

有限状态自动机（Deterministic Finite Automaton，DFA）是由

  1. 状态集合 ；
  2. 字符集 ；
  3. 状态转移函数 ，即 ；
  4. 一个开始状态 ；
  5. 一个接收的状态集合 。

组成的五元组 。

如果用 AC 自动机理解，状态集合就是字典树（图）的结点；字符集就是 a 到 z（或者更多）；状态转移函数就是  的函数（即 ）；开始状态就是字典树的根结点；接收状态就是你在字典树中标记的字符串结尾结点组成的集合。

KMP 自动机

KMP 自动机就是一个不断读入待匹配串，每次匹配时走到接受状态的 DFA。如果共有  个状态，第  个状态表示已经匹配了前  个字符。我们定义  表示状态  读入字符  后到达的状态， 表示 prefix function，则有：

（约定 ）

我们发现  只依赖于之前的值，所以可以跟 KMP 一起求出来。

需要注意走到接受状态之后应该立即转移到该状态的 next。

时间和空间复杂度：。

AC 自动机是 以 Trie 的结构为基础，结合 KMP 的思想 建立的自动机，用于解决多模式匹配等任务。

AC 自动机本质上是 Trie 上的自动机。

在阅读本文之前，请先阅读 KMP 和 Trie。

 

解释

简单来说，建立一个 AC 自动机有两个步骤：

 

  1. 基础的 Trie 结构：将所有的模式串构成一棵 Trie。
  2. KMP 的思想：对 Trie 树上所有的结点构造失配指针。

建立完毕后，就可以利用它进行多模式匹配。

 

字典树构建

AC 自动机在初始时会将若干个模式串插入到一个 Trie 里，然后在 Trie 上建立 AC 自动机。这个 Trie 就是普通的 Trie，按照 Trie 原本的建树方法建树即可。

需要注意的是，Trie 中的结点表示的是某个模式串的前缀。我们在后文也将其称作状态。一个结点表示一个状态，Trie 的边就是状态的转移。

形式化地说，对于若干个模式串 ，将它们构建一棵字典树后的所有状态的集合记作 。

 

失配指针

AC 自动机利用一个 fail 指针来辅助多模式串的匹配。

状态  的 fail 指针指向另一个状态 ，其中 ，且  是  的最长后缀（即在若干个后缀状态中取最长的一个作为 fail 指针）。

fail 指针与 KMP 中的 next 指针相比：

 

  1. 共同点：两者同样是在失配的时候用于跳转的指针。
  2. 不同点：next 指针求的是最长 Border（即最长的相同前后缀），而 fail 指针指向所有模式串的前缀中匹配当前状态的最长后缀。

因为 KMP 只对一个模式串做匹配，而 AC 自动机要对多个模式串做匹配。有可能 fail 指针指向的结点对应着另一个模式串，两者前缀不同。

总结下来，AC 自动机的失配指针指向当前状态的最长后缀状态。

注意：AC 自动机在做匹配时，同一位上可匹配多个模式串。

 

构建指针

下面介绍构建 fail 指针的 基础思想：

构建 fail 指针，可以参考 KMP 中构造 Next 指针的思想。

考虑字典树中当前的结点 ， 的父结点是 ， 通过字符 c 的边指向 ，即 。假设深度小于  的所有结点的 fail 指针都已求得。

 

  1. 如果  存在：则让 u 的 fail 指针指向 。相当于在  和  后面加一个字符 c，分别对应  和 。
  2. 如果  不存在：那么我们继续找到 。重复 1 的判断过程，一直跳 fail 指针直到根结点。
  3. 如果依然不存在，就让 fail 指针指向根结点。

如此即完成了  的构建。

 

例子

下面将使用若干张 GIF 动图来演示对字符串 i he his she hers 组成的字典树构建 fail 指针的过程：

 

  1. 黄色结点：当前的结点 。
  2. 绿色结点：表示已经 BFS 遍历完毕的结点，
  3. 橙色的边：fail 指针。
  4. 红色的边：当前求出的 fail 指针。

AC_automation_gif_b_3.gif

我们重点分析结点 6 的 fail 指针构建：

AC_automation_6_9.png

找到 6 的父结点 5，。然而 10 结点没有字母 s 连出的边；继续跳到 10 的 fail 指针，。发现 0 结点有字母 s 连出的边，指向 7 结点；所以 。

下图展示了构建完毕的状态：

finish

字典树与字典图

关注构建函数 build()，该函数的目标有两个，一个是构建 fail 指针，一个是构建自动机。参数如下：

 

  1. tr[u,c]：有两种理解方式。我们可以简单理解为字典树上的一条边，即 ；也可以理解为从状态（结点） 后加一个字符 c 到达的状态（结点），即一个状态转移函数 。为了方便，下文中我们将用第二种理解方式。
  2. 队列 q：用于 BFS 遍历字典树。
  3. fail[u]：结点  的 fail 指针。

实现

C++

Python

void build() {
  for (int i = 0; i < 26; i++)
    if (tr[0][i]) q.push(tr[0][i]);
  while (q.size()) {
    int u = q.front();
    q.pop();
    for (int i = 0; i < 26; i++) {
      if (tr[u][i])
        fail[tr[u][i]] = tr[fail[u]][i], q.push(tr[u][i]);
      else
        tr[u][i] = tr[fail[u]][i];
    }
  }
}

解释

build 函数将结点按 BFS 顺序入队，依次求 fail 指针。这里的字典树根结点为 0，我们将根结点的子结点一一入队。若将根结点入队，则在第一次 BFS 的时候，会将根结点儿子的 fail 指针标记为本身。因此我们将根结点的儿子一一入队，而不是将根结点入队。

然后开始 BFS：每次取出队首的结点 u（ 在之前的 BFS 过程中已求得），然后遍历字符集（这里是 0-25，对应 a-z，即  的各个子节点）：

  1. 如果  存在，我们就将  的 fail 指针赋值为 。根据之前的描述，我们应该用 while 循环，不停的跳 fail 指针，判断是否存在字符 i 对应的结点，然后赋值，但此处通过特殊处理简化了这些代码。
  2. 否则，令  指向  的状态。

这里的处理是，通过 else 语句的代码修改字典树的结构，将不存在的字典树的状态链接到了失配指针的对应状态。在原字典树中，每一个结点代表一个字符串 ，是某个模式串的前缀。而在修改字典树结构后，尽管增加了许多转移关系，但结点（状态）所代表的字符串是不变的。

而  相当于是在  后添加一个字符 c 变成另一个状态 。如果  存在，说明存在一个模式串的前缀是 ，否则我们让  指向 。由于  对应的字符串是  的后缀，因此  对应的字符串也是  的后缀。

换言之在 Trie 上跳转的时侯，我们只会从  跳转到 ，相当于匹配了一个 ；但在 AC 自动机上跳转的时侯，我们会从  跳转到  的后缀，也就是说我们匹配一个字符 c，然后舍弃  的部分前缀。舍弃前缀显然是能匹配的。同时如果文本串能匹配 ，显然它也能匹配  的后缀，所以 fail 指针同样在舍弃前缀。所谓的 fail 指针其实就是  的一个后缀集合。

tr 数组还有另一种比较简单的理解方式：如果在位置  失配，我们会跳转到  的位置。注意这会导致我们可能沿着 fail 数组跳转多次才能来到下一个能匹配的位置。所以我们可以用 tr 数组直接记录记录下一个能匹配的位置，这样对程序的性能有一定的优化。

此处对字典树结构的修改，可以使得匹配转移更加完善。同时它将 fail 指针跳转的路径做了压缩，使得本来需要跳很多次 fail 指针变成跳一次。

过程

这里依然用若干张 GIF 动图展示构建过程：

AC_automation_gif_b_pro3.gif

  1. 蓝色结点：BFS 遍历到的结点 u
  2. 蓝色的边：当前结点下，AC 自动机修改字典树结构连出的边。
  3. 黑色的边：AC 自动机修改字典树结构连出的边。
  4. 红色的边：当前结点求出的 fail 指针
  5. 黄色的边：fail 指针
  6. 灰色的边：字典树的边

可以发现，众多交错的黑色边将字典树变成了 字典图。图中省略了连向根结点的黑边（否则会更乱）。我们重点分析一下结点 5 遍历时的情况。我们求  的 fail 指针：

AC_automation_b_7.png

本来的策略是找 fail 指针，于是我们跳到  发现没有 s 连出的字典树的边，于是跳到 ，发现有 ，于是 ；但是有了黑边、蓝边，我们跳到  之后直接走  就走到  号结点了。

这就是 build 完成的两件事：构建 fail 指针和建立字典图。这个字典图也会在查询的时候起到关键作用。

多模式匹配

接下来分析匹配函数 query()：

实现

C++

Python

int query(char *t) {
  int u = 0, res = 0;
  for (int i = 1; t[i]; i++) {
    u = tr[u][t[i] - 'a'];  // 转移
    for (int j = u; j && e[j] != -1; j = fail[j]) {
      res += e[j], e[j] = -1;
    }
  }
  return res;
}

解释

这里  作为字典树上当前匹配到的结点，res 即返回的答案。循环遍历匹配串， 在字典树上跟踪当前字符。利用 fail 指针找出所有匹配的模式串，累加到答案中。然后清零。在上文中我们分析过，字典树的结构其实就是一个 trans 函数，而构建好这个函数后，在匹配字符串的过程中，我们会舍弃部分前缀达到最低限度的匹配。fail 指针则指向了更多的匹配状态。最后上一份图。对于刚才的自动机：

AC_automation_b_13.png

我们从根结点开始尝试匹配 ushersheishis，那么  的变化将是：

AC_automation_gif_c.gif

  1. 红色结点： 结点
  2. 粉色箭头： 在自动机上的跳转，
  3. 蓝色的边：成功匹配的模式串
  4. 蓝色结点：示跳 fail 指针时的结点（状态）。

效率优化

题目请参考洛谷 P5357【模板】AC 自动机（二次加强版）

因为我们的 AC 自动机中，每次匹配，会一直向 fail 边跳来找到所有的匹配，但是这样的效率较低，在某些题目中会超时。

那么我们如何优化呢？首先我们需要了解 fail 指针的一个性质：一个 AC 自动机中，如果只保留 fail 边，那么剩余的图一定是一棵树。

这是显然的，因为 fail 不会成环，且深度一定比现在低，所以得证。

而我们 AC 自动机的匹配就可以转化为在 fail 树上的链求和问题。

所以我们只需要优化一下这部分就可以了。

我们这里提供两种思路。

拓扑排序优化建图

观察到时间主要浪费在在每次都要跳 fail。如果我们可以预先记录，最后一并求和，那么效率就会优化。

于是我们按照 fail 树建图（注意不用真的建，只需要记录入度）：

建图

void getfail()  // 实际上也可以叫 build
{
  for (int i = 0; i < 26; i++) trie[0].son[i] = 1;
  q.push(1);
  trie[1].fail = 0;
  while (!q.empty()) {
    int u = q.front();
    q.pop();
    int Fail = trie[u].fail;
    for (int i = 0; i < 26; i++) {
      int v = trie[u].son[i];
      if (!v) {
        trie[u].son[i] = trie[Fail].son[i];
        continue;
      }
      trie[v].fail = trie[Fail].son[i];
      indeg[trie[Fail].son[i]]++;  // 修改点在这里，增加了入度记录
      q.push(v);
    }
  }
}

然后我们在查询的时候就可以只为找到节点的 ans 打上标记，在最后再用拓扑排序求出答案。

查询

void query(char *s) {
  int u = 1, len = strlen(s);
  for (int i = 0; i < len; i++) u = trie[u].son[s[i] - 'a'], trie[u].ans++;
}

void topu() {
  for (int i = 1; i <= cnt; i++)
    if (!indeg[i]) q.push(i);
  while (!q.empty()) {
    int fr = q.front();
    q.pop();
    vis[trie[fr].flag] = trie[fr].ans;
    int u = trie[fr].fail;
    trie[u].ans += trie[fr].ans;
    if (!(--indeg[u])) q.push(u);
  }
}

最后是主函数：

主函数

int main() {
  // do_something();
  scanf("%s", s);
  query(s);
  topu();
  for (int i = 1; i <= n; i++) cout << vis[rev[i]] << std::endl;
  // do_another_thing();
}

完整代码

Luogu P5357【模板】AC 自动机（二次加强版）

// Code by rickyxrc | https://www.luogu.com.cn/record/115706921
#include <bits/stdc++.h>
#define maxn 8000001
using namespace std;
char s[maxn];
int n, cnt, vis[maxn], rev[maxn], indeg[maxn], ans;

struct trie_node {
  int son[27];
  int fail;
  int flag;
  int ans;

  void init() {
    memset(son, 0, sizeof(son));
    fail = flag = 0;
  }
} trie[maxn];

queue<int> q;

void init() {
  for (int i = 0; i <= cnt; i++) trie[i].init();
  for (int i = 1; i <= n; i++) vis[i] = 0;
  cnt = 1;
  ans = 0;
}

void insert(char *s, int num) {
  int u = 1, len = strlen(s);
  for (int i = 0; i < len; i++) {
    int v = s[i] - 'a';
    if (!trie[u].son[v]) trie[u].son[v] = ++cnt;
    u = trie[u].son[v];
  }
  if (!trie[u].flag) trie[u].flag = num;
  rev[num] = trie[u].flag;
  return;
}

void getfail(void) {
  for (int i = 0; i < 26; i++) trie[0].son[i] = 1;
  q.push(1);
  trie[1].fail = 0;
  while (!q.empty()) {
    int u = q.front();
    q.pop();
    int Fail = trie[u].fail;
    for (int i = 0; i < 26; i++) {
      int v = trie[u].son[i];
      if (!v) {
        trie[u].son[i] = trie[Fail].son[i];
        continue;
      }
      trie[v].fail = trie[Fail].son[i];
      indeg[trie[Fail].son[i]]++;
      q.push(v);
    }
  }
}

void topu() {
  for (int i = 1; i <= cnt; i++)
    if (!indeg[i]) q.push(i);
  while (!q.empty()) {
    int fr = q.front();
    q.pop();
    vis[trie[fr].flag] = trie[fr].ans;
    int u = trie[fr].fail;
    trie[u].ans += trie[fr].ans;
    if (!(--indeg[u])) q.push(u);
  }
}

void query(char *s) {
  int u = 1, len = strlen(s);
  for (int i = 0; i < len; i++) u = trie[u].son[s[i] - 'a'], trie[u].ans++;
}

int main() {
  scanf("%d", &n);
  init();
  for (int i = 1; i <= n; i++) scanf("%s", s), insert(s, i);
  getfail();
  scanf("%s", s);
  query(s);
  topu();
  for (int i = 1; i <= n; i++) cout << vis[rev[i]] << std::endl;
  return 0;
}

子树求和

和拓扑排序的思路接近，我们预先将子树求和，询问时直接累加和值即可。

完整代码请见总结模板 3。

AC 自动机上 DP

这部分将以 P2292 [HNOI2004] L 语言 为例题讲解。

不难想到一个朴素的思路：建立 AC 自动机，在 AC 自动机上对于所有 fail 指针的子串转移，最后取最大值得到答案。

主要代码如下。若不熟悉代码中的类型定义，可以先看末尾的完整代码：

查询部分主要代码


 
void query(char *s) {
  int u = 1, len = strlen(s), l = 0;
  for (int i = 0; i < len; i++) {
    int v = s[i] - 'a';
    int k = trie[u].son[v];
    while (k > 1) {
      if (trie[k].flag && (dp[i - trie[k].len] || i - trie[k].len == -1))
        dp[i] = dp[i - trie[k].len] + trie[k].len;
      k = trie[k].fail;
    }
    u = trie[u].son[v];
  }
}

主函数里取 max 即可。

1

for (int i = 0, e = strlen(T); i < e; i++) mx = std::max(mx, dp[i]);

但是这样的思路复杂度不是线性（因为要跳每个节点的 fail），会在第二个子任务中超时，所以我们需要进行优化。

我们再看看题目的特殊性质，我们发现所有单词的长度只有 ，所以可以想到状态压缩优化。

我们发现，目前的时间瓶颈主要在跳 fail 这一步，如果我们可以将这一步优化到 ，就可以保证整个问题在严格线性的时间内被解出。

我们可以将前  位字母中，可能的子串长度存下来，并压缩到状态中，存在每个子节点中。

那么我们在 buildfail 的时候就可以这么写：

构建 fail 指针

  
void getfail(void) {
  for (int i = 0; i < 26; i++) trie[0].son[i] = 1;
  q.push(1);
  trie[1].fail = 0;
  while (!q.empty()) {
    int u = q.front();
    q.pop();
    int Fail = trie[u].fail;
    // 对状态的更新在这里
    trie[u].stat = trie[Fail].stat;
    if (trie[u].flag) trie[u].stat |= 1 << trie[u].depth;
    for (int i = 0; i < 26; i++) {
      int v = trie[u].son[i];
      if (!v)
        trie[u].son[i] = trie[Fail].son[i];
      else {
        trie[v].depth = trie[u].depth + 1;
        trie[v].fail = trie[Fail].son[i];
        q.push(v);
      }
    }
  }
}

然后查询时就可以去掉跳 fail 的循环，将代码简化如下：

查询


 
int query(char *s) {
  int u = 1, len = strlen(s), mx = 0;
  unsigned st = 1;
  for (int i = 0; i < len; i++) {
    int v = s[i] - 'a';
    u = trie[u].son[v];
    // 因为往下跳了一位每一位的长度都+1
    st <<= 1;
    // 这里的 & 值是状压 dp 的使用，代表两个长度集的交非空
    if (trie[u].stat & st) st |= 1, mx = i + 1;
  }
  return mx;
}

我们的 trie[u].stat 维护的是从 u 节点开始，整条 fail 链上的长度集（因为长度集小于 32 所以不影响），而 st 则维护的是查询字符串走到现在，前 32 位（因为状态压缩自然溢出）的长度集。

& 值不为 0，则代表两个长度集的交集非空，我们此时就找到了一个匹配。

完整代码

P2292 [HNOI2004] L 语言

// Code by rickyxrc | https://www.luogu.com.cn/record/115806238
#include <stdio.h>
#include <string.h>

#include <queue>
#define maxn 3000001
char T[maxn];
int n, cnt, vis[maxn], ans, m, dp[maxn];

struct trie_node {
  int son[26];
  int fail, flag, depth;
  unsigned stat;

  void init() {
    memset(son, 0, sizeof(son));
    fail = flag = depth = 0;
  }
} trie[maxn];

std::queue<int> q;

void init() {
  for (int i = 0; i <= cnt; i++) trie[i].init();
  for (int i = 1; i <= n; i++) vis[i] = 0;
  cnt = 1;
  ans = 0;
}

void insert(char *s, int num) {
  int u = 1, len = strlen(s);
  for (int i = 0; i < len; i++) {
    // trie[u].depth = i + 1;
    int v = s[i] - 'a';
    if (!trie[u].son[v]) trie[u].son[v] = ++cnt;
    u = trie[u].son[v];
  }
  trie[u].flag = num;
  // trie[u].stat = 1;
  // printf("set %d stat %d\n", u-1, 1);
  return;
}

void getfail(void) {
  for (int i = 0; i < 26; i++) trie[0].son[i] = 1;
  q.push(1);
  trie[1].fail = 0;
  while (!q.empty()) {
    int u = q.front();
    q.pop();
    int Fail = trie[u].fail;
    trie[u].stat = trie[Fail].stat;
    if (trie[u].flag) trie[u].stat |= 1 << trie[u].depth;
    for (int i = 0; i < 26; i++) {
      int v = trie[u].son[i];
      if (!v)
        trie[u].son[i] = trie[Fail].son[i];
      else {
        trie[v].depth = trie[u].depth + 1;
        trie[v].fail = trie[Fail].son[i];
        q.push(v);
      }
    }
  }
}

int query(char *s) {
  int u = 1, len = strlen(s), mx = 0;
  unsigned st = 1;
  for (int i = 0; i < len; i++) {
    int v = s[i] - 'a';
    u = trie[u].son[v];
    st <<= 1;
    if (trie[u].stat & st) st |= 1, mx = i + 1;
  }
  return mx;
}

int main() {
  scanf("%d%d", &n, &m);
  init();
  for (int i = 1; i <= n; i++) {
    scanf("%s", T);
    insert(T, i);
  }
  getfail();
  for (int i = 1; i <= m; i++) {
    scanf("%s", T);
    printf("%d\n", query(T));
  }
}

总结

时间复杂度：定义  是模板串的长度， 是文本串的长度， 是字符集的大小（常数，一般为 26）。如果连了 trie 图，时间复杂度就是 ，其中  是 AC 自动机中结点的数目，并且最大可以达到 。如果不连 trie 图，并且在构建 fail 指针的时候避免遍历到空儿子，时间复杂度就是 。

模板 1

Luogu P3808【模板】AC 自动机（简单版）

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 6;
int n;

namespace AC {
int tr[N][26], tot;
int e[N], fail[N];

void insert(char *s) {
  int u = 0;
  for (int i = 1; s[i]; i++) {
    if (!tr[u][s[i] - 'a']) tr[u][s[i] - 'a'] = ++tot;  // 如果没有则插入新节点
    u = tr[u][s[i] - 'a'];                              // 搜索下一个节点
  }
  e[u]++;  // 尾为节点 u 的串的个数
}

queue<int> q;

void build() {
  for (int i = 0; i < 26; i++)
    if (tr[0][i]) q.push(tr[0][i]);
  while (q.size()) {
    int u = q.front();
    q.pop();
    for (int i = 0; i < 26; i++) {
      if (tr[u][i]) {
        fail[tr[u][i]] =
            tr[fail[u]][i];  // fail数组：同一字符可以匹配的其他位置
        q.push(tr[u][i]);
      } else
        tr[u][i] = tr[fail[u]][i];
    }
  }
}

int query(char *t) {
  int u = 0, res = 0;
  for (int i = 1; t[i]; i++) {
    u = tr[u][t[i] - 'a'];  // 转移
    for (int j = u; j && e[j] != -1; j = fail[j]) {
      res += e[j], e[j] = -1;
    }
  }
  return res;
}
}  // namespace AC

char s[N];

int main() {
  scanf("%d", &n);
  for (int i = 1; i <= n; i++) scanf("%s", s + 1), AC::insert(s);
  scanf("%s", s + 1);
  AC::build();
  printf("%d", AC::query(s));
  return 0;
}

模板 2

Luogu P3796【模板】AC 自动机（加强版）

#include <bits/stdc++.h>
using namespace std;
const int N = 156, L = 1e6 + 6;

namespace AC {
const int SZ = N * 80;
int tot, tr[SZ][26];
int fail[SZ], idx[SZ], val[SZ];
int cnt[N];  // 记录第 i 个字符串的出现次数

void init() {
  memset(fail, 0, sizeof(fail));
  memset(tr, 0, sizeof(tr));
  memset(val, 0, sizeof(val));
  memset(cnt, 0, sizeof(cnt));
  memset(idx, 0, sizeof(idx));
  tot = 0;
}

void insert(char *s, int id) {  // id 表示原始字符串的编号
  int u = 0;
  for (int i = 1; s[i]; i++) {
    if (!tr[u][s[i] - 'a']) tr[u][s[i] - 'a'] = ++tot;
    u = tr[u][s[i] - 'a'];  // 转移
  }
  idx[u] = id;  // 以 u 为结尾的字符串编号为 idx[u]
}

queue<int> q;

void build() {
  for (int i = 0; i < 26; i++)
    if (tr[0][i]) q.push(tr[0][i]);
  while (q.size()) {
    int u = q.front();
    q.pop();
    for (int i = 0; i < 26; i++) {
      if (tr[u][i]) {
        fail[tr[u][i]] =
            tr[fail[u]][i];  // fail数组：同一字符可以匹配的其他位置
        q.push(tr[u][i]);
      } else
        tr[u][i] = tr[fail[u]][i];
    }
  }
}

int query(char *t) {  // 返回最大的出现次数
  int u = 0, res = 0;
  for (int i = 1; t[i]; i++) {
    u = tr[u][t[i] - 'a'];
    for (int j = u; j; j = fail[j]) val[j]++;
  }
  for (int i = 0; i <= tot; i++)
    if (idx[i]) res = max(res, val[i]), cnt[idx[i]] = val[i];
  return res;
}
}  // namespace AC

int n;
char s[N][100], t[L];

int main() {
  while (~scanf("%d", &n)) {
    if (n == 0) break;
    AC::init();  // 数组清零
    for (int i = 1; i <= n; i++)
      scanf("%s", s[i] + 1), AC::insert(s[i], i);  // 需要记录该字符串的序号
    AC::build();
    scanf("%s", t + 1);
    int x = AC::query(t);
    printf("%d\n", x);
    for (int i = 1; i <= n; i++)
      if (AC::cnt[i] == x) printf("%s\n", s[i] + 1);
  }
  return 0;
}

模版 3

Luogu P5357【模板】AC 自动机（二次加强版）


 
#include <deque>
#include <iostream>

void promote() {
  std::ios::sync_with_stdio(0);
  std::cin.tie(0);
  std::cout.tie(0);
  return;
}

typedef char chr;
typedef std::deque<int> dic;

const int maxN = 2e5;
const int maxS = 2e5;
const int maxT = 2e6;

int n;
chr s[maxS + 10];
chr t[maxT + 10];
int cnt[maxN + 10];

struct AhoCorasickAutomaton {
  struct Node {
    int son[30];
    int val;
    int fail;
    int head;
    dic index;
  } node[maxS + 10];

  struct Edge {
    int head;
    int next;
  } edge[maxS + 10];

  int root;
  int ncnt;
  int ecnt;

  void Insert(chr *str, int i) {
    int u = root;
    for (int i = 1; str[i]; i++) {
      if (node[u].son[str[i] - 'a' + 1] == 0)
        node[u].son[str[i] - 'a' + 1] = ++ncnt;
      u = node[u].son[str[i] - 'a' + 1];
    }
    node[u].index.push_back(i);
    return;
  }

  void Build() {
    dic q;
    for (int i = 1; i <= 26; i++)
      if (node[root].son[i]) q.push_back(node[root].son[i]);
    while (!q.empty()) {
      int u = q.front();
      q.pop_front();
      for (int i = 1; i <= 26; i++) {
        if (node[u].son[i]) {
          node[node[u].son[i]].fail = node[node[u].fail].son[i];
          q.push_back(node[u].son[i]);
        } else {
          node[u].son[i] = node[node[u].fail].son[i];
        }
      }
    }
    return;
  }

  void Query(chr *str) {
    int u = root;
    for (int i = 1; str[i]; i++) {
      u = node[u].son[str[i] - 'a' + 1];
      node[u].val++;
    }
    return;
  }

  void addEdge(int tail, int head) {
    ecnt++;
    edge[ecnt].head = head;
    edge[ecnt].next = node[tail].head;
    node[tail].head = ecnt;
    return;
  }

  void DFS(int u) {
    for (int e = node[u].head; e; e = edge[e].next) {
      int v = edge[e].head;
      DFS(v);
      node[u].val += node[v].val;
    }
    for (auto i : node[u].index) cnt[i] += node[u].val;
    return;
  }

  void FailTree() {
    for (int u = 1; u <= ncnt; u++) addEdge(node[u].fail, u);
    DFS(root);
    return;
  }
} ACM;

int main() {
  std::cin >> n;
  for (int i = 1; i <= n; i++) {
    std::cin >> (s + 1);
    ACM.Insert(s, i);
  }
  ACM.Build();
  std::cin >> (t + 1);
  ACM.Query(t);
  ACM.FailTree();
  for (int i = 1; i <= n; i++) std::cout << cnt[i] << '\n';
  return 0;
}

拓展

确定有限状态自动机

作为拓展延伸，文末我们简单介绍一下 自动机 与 KMP 自动机。

有限状态自动机（Deterministic Finite Automaton，DFA）是由

  1. 状态集合 ；
  2. 字符集 ；
  3. 状态转移函数 ，即 ；
  4. 一个开始状态 ；
  5. 一个接收的状态集合 。

组成的五元组 。

如果用 AC 自动机理解，状态集合就是字典树（图）的结点；字符集就是 a 到 z（或者更多）；状态转移函数就是  的函数（即 ）；开始状态就是字典树的根结点；接收状态就是你在字典树中标记的字符串结尾结点组成的集合。

KMP 自动机

KMP 自动机就是一个不断读入待匹配串，每次匹配时走到接受状态的 DFA。如果共有  个状态，第  个状态表示已经匹配了前  个字符。我们定义  表示状态  读入字符  后到达的状态， 表示 prefix function，则有：

（约定 ）

我们发现  只依赖于之前的值，所以可以跟 KMP 一起求出来。

需要注意走到接受状态之后应该立即转移到该状态的 next。

时间和空间复杂度：。

 

刘瑾瑜在2024-10-05 09:30:29追加了内容

抱歉各位，从铁榔头看见的，原网址忘了

刘瑾瑜在2024-10-05 09:31:49追加了内容

感谢，原网址https://www.luogu.com.cn/article/7lbmr2xt

举报

10酷町豆 代码分享 0条评论 1 月，2 周 前

0
0
0
0
李北辰
李北辰
初级光能
初级光能

我看完了以后：……AC自动机是啥？

阅读更多
举报

1 月，2 周 前 0条评论

0
0
0
毕博雨
毕博雨
中级光能
中级光能

好像在哪里见过······

真的是你写的吗？（分支结构）

if(是自己写的){

没想到是这样的！

}else{

}

（无恶意，抄袭没什么厉害的）

阅读更多
举报

1 月，2 周 前 4条评论

0
於海洋
於海洋
高级光能
高级光能

就是抄的呀，在Google上搜一下就出来了

是不是想精品贴想疯了，还是想装b想疯了

阅读更多
举报

1 月，2 周 前 0条评论

0
包思远
包思远
新手启示者
新手启示者

抄的其实发个网址就行了。。。。。。

阅读更多
举报

1 月，2 周 前 1条评论

0
葛子豪
葛子豪
高级光能
高级光能

emm……好像还是没听懂

阅读更多
举报

1 月，2 周 前 0条评论

我要回答
© 2021 酷町堂教育机构 版权所有 皖ICP备16015773号-1