问题标题: 酷町堂：萌新求助QAQ(๑•́ ₃ •̀๑)

Question

2

已解决

陆麟瑞

资深天翼

刚学数位dp，请问有哪些关于数位dp的题目。

还有为什么数位dp偏偏得用记忆化搜索来写？

不要在网上抄QAQ

酷町豆刷题求解 C++ 14条评论 6 年，3 月前

Answer 1

已采纳

陈胤廷

修练者

题目链接：hdu 2089 不要62
题目大意是统计【A，B】区间内没有4并且没有62的数，因为有之前那道题的铺垫，很快想到了解决方法。
思路： 预处理一个dp数组，dp【i，j】代表最高位为 j 的 i 位数满足题述要求的的个数；然后分别统计【0，B】和【0，A-1】区间内满足条件的数——与之前那题类似，不过更简单了。

题目链接：BZOJ 1833

解题思路：
非常常规的一道数位DP题目，然而，因为好久没做过题，结果怒调了三个钟。关键的地方在于数字0的处理，我采用的做法是先不考虑特殊的0，处理完别的数字之后，使用直接推公式的方法直接求得0的个数。注意数据范围，得使用long long。

题目链接：HDU 3652

解题思路：
数位DP，状态 dp[i][j][k][c]表示 i 位数中，以 j 开头的，模13为k的数的统计情况，其中 c 可取0或者1，0表示不包含13，1表示包含，这样我们就可以把所有的数分成两部分，设计状态转移方程。

题目链接：hihoCoder 1033

解题思路：
思路超级简单，就是单纯的数位DP，但是，还是觉得好恶心。需要特殊考虑的就是第一位数字为0的情况，不能直接把状态转移的结果拿出来。
状态：dp[i][j][k+100]，i 位数中以 j 开头的数交叉和为k的数量
（这里因为k有可能取负数，所以需要让它变正，加100即可）

Answer 2

郑砺锋

新手守护

不懂

Answer 3

蒋智航

高级天翼

你不是已经学完DP了吗？

分割线

————————————————————————————————————

你到底多少豆子啊，不停的换头像。

蒋智航在2018-08-20 14:09:03追加了内容

∵数位dp要用记忆化搜索来写

∴数位dp得用记忆化搜索来写

皮一下

Answer 4

王子凡

高级光能

陆dalao，你问的问题，辣沫深奥，我们这些zz怎么会呢

王子凡在2018-08-20 14:19:47追加了内容

陆麟瑞

Answer 5

周建勋

中级光能

俺也不知道！！！

呵呵！！！

Answer 6

王文博

缔造者之神

1

Answer 7

王光裕

资深光能

不懂

Answer 8

项依凡

初级光能

https://daohang.qq.com/?unc=Af31009

项依凡在2018-08-21 20:42:01追加了内容

陆麟瑞

项依凡在2018-08-21 20:42:29追加了内容

这是王子凡的

项依凡在2018-08-21 20:43:00追加了内容

这是王子凡的，但是也能代表我

Answer 9

何羽凡

修练者

不懂

Answer 10

王泽轩

资深天翼

1

Answer 11

尹宗鑫

新手守护

能量宝石：

输入n,在输入n个正整数，求最大连续的和

尹宗鑫在2018-08-23 09:37:57追加了内容

***一定要先按照x从小到大排序（这样去掉后效性，你的合伙人只在你的一个方向上），再求y的最长子序列。

1,4

2,4

3,4

4,4

1,3

2，3

3，3

4,3

1,2

2,2

3,2

4,2

1,1

2,1

3,1

4,1

k =6

记忆数组

路径

1

1,1

1 3

2

2,3

2 2

6

3

3,1

1 2

5

4

3,2

2 2

5

4,3

3 1

-1

6

4,4

3 1

-1

先读k条斜线：---尽可能走斜线

方法是：先把每条斜线按照x坐标从小到大排列（去掉后效性可以用dp），

x-y都必须严格递增才能走

1 1----f[1]=1

1 3----f[2]=1+0=1

3 1----f[3]=1+0=1错误了，你的合伙人既在前又在后，永远填不了

2 4----f[4]=1+

3 5

---排序后为：

k=3;最多可以选3条

1 1----f[1]=1

1 3----f[2]=1+0=1

2 4----f[3]=1+1=2

3 1----f[4]=1+0=1

3 5----f[5]=1+2=3

最多可以走:t条

少走直线：2*t

最后的代价： t*sqrt(2)*100+ 100* (m+n-2*t)

Answer 12

陈胤廷

修练者

1. 动态规划

动态规划是运筹学的一个方向，就是把多级最优化问题分解成一系列的单阶问题。在不断增加的过程中，不断的计算当前问题的最优解。

一般分为如下四个部分：

线性动规：拦截导弹，合唱队形，挖地雷，建学校，剑客决斗等；
区域动规：石子合并，加分二叉树，统计单词个数，炮兵布阵等；
树形动规：贪吃的九头龙，二分查找树，聚会的欢乐，数字三角形等；
背包问题：01背包问题，完全背包问题，分组背包问题，二维背包，装箱问题，挤牛奶（同济ACM第1132题）等；

2. 汽车生产线问题

这个问题是《算法导论》的动态规划的例题，我自己觉得这道题比较简单而且典型，所以就解释下这个题目：

Colonel汽车公司在有两条装配线的工厂里生成汽车。每一条装配线上有n个装配站，两条生产线上相同位置的装配站功能相同，但所需时间不同，并且汽车底盘在两条装配线间转移要花费一定的时间。如下图所示两条生产线。

装配线图

首先我们知道每个阶段的最短时间，都包含了上一阶段的最短时间。
而比较简单的是，我们只有两种情况，一种是在装配线1上时间短，一种是在装配线2上时间短。
假如暴力搜索，贪心去算得话（也就是递归的办法）。时间复杂就是2^n，这个是不可接受的。

这个时候我们的办法是先从第一个问题开始，装配线1, 2上只有一个station。那么比较简单，一比较就好了。当有两个station的时候，就是从上一次比较的结果中(一个line 1最短，一个line 2最短)中继续加上当前station的值继续比较。

所以我们发现是每个当前的最优解，都包含了上一次的最优解。

3. 代码

代码就是我们从最开始，一直保存当前问题的最优解，然后去求的下一次的最优解。

//
//  main.cpp
//  DP_line
//
//  Created by Alps on 15/4/26.
//  Copyright (c) 2015年 chen. All rights reserved.
//

#include <iostream>
using namespace std;

#define NUM 5

int main(){
    int first[NUM];//到装备站1,i的最短路径长度
    int second[NUM];//到装配站2,i的最短路径长度
    int linef[NUM]; //从1进入的路径
    int lines[NUM]; //从2进入的路径
    int a[NUM]; //在装配站1,i 所需要呆的时间
    int b[NUM]; //再装配站2,i 所需要呆的时间
    int m[NUM]; //从装配站1,i-1 到装配站2,i的时间
    int n[NUM]; //从装配站2,i-1 到装配站1,i的时间
    int line[NUM]; //当前最短路经所经过的装配站
    int f[NUM]; //当前最短路径长度
    int ea,eb,xa,xb; // ea为进入装配站1时间，eb为进入2的时间，xa为出装配站1的时间，xb为出装配站2的

    scanf("%d %d %d %d",&ea,&eb,&xa,&xb);
    for(int i=0;i<NUM;++i)
    {
        scanf("%d %d", &a[i], &b[i]);
    }
    first[0] = ea + a[0];
    second[0] = eb + b[0];
    for(int i=0;i<NUM-1;++i)
    {
        scanf("%d %d", &m[i], &n[i]);
    }
    for(int i=1;i<NUM;++i)
    {
        if(first[i-1] + a[i] < second[i-1] + m[i-1] + a[i])
        {
            first[i] = first[i-1] + a[i];
            linef[i] = 1;
        }else{
            first[i] = second[i-1] + m[i-1] + a[i];
            linef[i] = 2;
        }
        if(second[i-1] + b[i] < first[i-1] + n[i-1] + b[i])
        {
            second[i] = second[i-1] + b[i];
            lines[i] = 2;
        }else
        {
            second[i] = first[i-1] + n[i-1] + b[i-1];
            lines[i] = 1;
        }
    }
    for(int i=0;i<NUM;++i)
    {
        if(first[i] + xa < second[i] + xb)
        {
            f[i] = first[i] + xa;
            line[i] = 1;
        }else{
            f[i] = second[i] + xb;
            line[i] = 2;
        }
    }

    for(int i=0;i<NUM;++i)
    {
        printf("station %d\n",line[i]);
    }
    printf("Distince is %d\n",f[NUM-1]);

    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

这个代码比较简单，精华就是那个for循环了。

测试用例如下：

1
2
3
4
5
6
7
8
9
10

假如有任何建议，欢迎评论。互相学习。谢谢。

Answer 13

陈胤廷

修练者

问题1：找硬币，换钱的方法

输入：

penny数组代表所有货币的面值，正数不重复
aim小于等于1000，代表要找的钱

输出：
换钱的方法总数

问题2：跳台阶问题：

其实是斐波那契问题，f(n)=f(n-1)+f(n-2)

问题3：走矩阵，求路劲最小和，或者是求整个路径

n×m的map，则 f(n,m)=min(f(n-1,m),f(n,m-1))+map[n][m]；
由于这里和问题1类似，可以只用到一个一维数组求解；

问题4：最长上升子序列问题（LIS）

解法：O（N方）用dp数组的dp[i]记录下以A[i]结尾的递增子序列中最长的长度，计算dp[i+1]时，遍历A[0~i]找到比A[i+1]小的元素，再比较与这些元素对应的dp数组中的值，找到最大的一个再加1，赋值给dp[i+1]。

问题5：最长公共子序列长度（LCS）

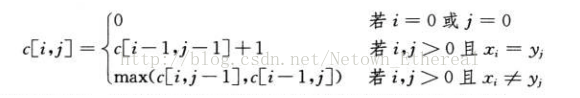
上图可以看出使用了斜侧的比较，所以不能再使用1维数组了

问题6：背包

N件物品，价值记录在数组V，重量记录在数组W，背包总重量最大为cap，要求总价值最大；

Answer 14

陈胤廷

修练者

望采纳！

陈胤廷在2018-08-24 19:28:39追加了内容

题目真确代码回头到家发给你。

Answer 15

李庚午

中级守护

数位DP，，，，，LLR巨佬您是要进省队啊。

不管了，以后看到LLR的问题全都先%%%再回答好了。

Answer 16

朱小川

缔造者

1

问题标题: 酷町堂：萌新求助QAQ(๑•́ ₃ •̀๑)

16 个回答: