问题标题: 差分约束

差分约束：线性规划矩阵A的每一行包含一个1与一个-1，其他元素为0.因此，由Ax<=b给出的约束条件是m个差分约束集合，其中包含n个未知元。每个约束条件为不等式：

                                                            xj-xi<=bk

其中1<=i,j<=n,i<=k<=m

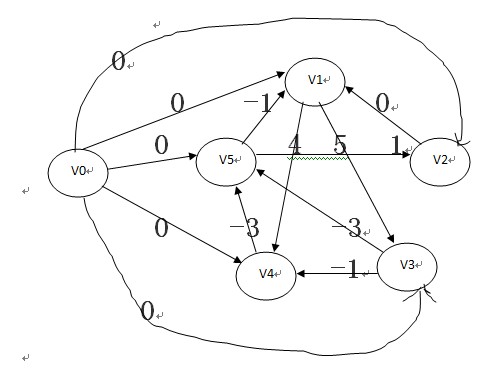
解决方法：把n个未知元看成n的有向图的顶点，xj-xi<=bk表示顶点j到顶点i长度为bk的有向线段。再添加一个v0顶点，与v0到其余顶点的有向线段，长度为0。（如下图）

可以证明 xi=β(v0,vi)(β(v0,vi)为顶点0到顶点i的最短路径长度）。所以就可以利用Bellman_Ford算求单源最短路径（不能用Dijkstra算法，因为有向线段长度可以为负）

// 差分约束系统.cpp : Defines the entry point for the console application.
//

#include "stdafx.h"
#include<iostream>
#define MAX 100
#define Infinity 65535
using namespace std;

//边的尾节点结构体
struct edgeNode
{
 int no; //边尾端的序号
 int weight; //边权值
 struct edgeNode * next; //下一个
};

//节点结构体
struct vexNode
{
 char info;  //节点名称
 struct edgeNode *link; //与之相连的端点
};

//存储节点信息
vexNode adjlist[MAX];
//前驱节点
int parent[MAX];
////源点到节点j最短路径的花费
int lowcost[MAX];
//差分矩阵
int  a[MAX][MAX];
//约束集
int w[MAX];

//根据差分矩阵建立邻接表存储
//adjlist为节点集，parent[j]为从0节点到节点j的最短路径的前驱节点
//lowcost[j]为从0节点到节点j的最短路径的代价
//w为输入的差分约束
//m，n分别为差分矩阵的行数和列数
void createGraph(vexNode *adjlist,int *parent,int *lowcost,int *w,int m,int n)
{
 int i,j;
 //初始化，节点vi的名称为char(a+i)
 for(i=0;i<=n;i++)
 {
  adjlist[i].info = (char)('a' + i);
  adjlist[i].link = NULL;
  lowcost[i] = Infinity;
  parent[i] = i;
 }
 int col1,col2;
 col1 = col2 = 0;
 edgeNode *p1;
 for(i=1;i<=m;i++)
 {
  for(j=1;j<=n;j++)
  {
   if(a[i][j]==-1)
    col1 = j;
   else if(a[i][j]==1)
    col2 = j;
  }
  p1 = (edgeNode*)malloc(sizeof(edgeNode));
  p1->no = col2;
  p1->weight = w[i];
  p1->next = adjlist[col1].link;
  adjlist[col1].link = p1;
 }
 for(i=1;i<=n;i++)
 {
  p1 = (edgeNode*)malloc(sizeof(edgeNode));
  p1->no = i;
  p1->weight = 0;
  p1->next = adjlist[0].link;
  adjlist[0].link = p1;
 }
 lowcost[0] = 0;
}

//寻找v0到，每一个节点的最短路径
bool Bellman_Ford(vexNode *adjlist,int *lowcost,int *parent,const int n)
{
 int i,j;
 for(j=0;j<n;j++)
 {
  for(i=0;i<=n;i++)
  {
   edgeNode *p1 = adjlist[i].link;
   while(p1 != NULL)
   {
    if(lowcost[i]+p1->weight <lowcost[p1->no])
    {
     lowcost[p1->no] = lowcost[i]+p1->weight;
     parent[p1->no] = i;
    }
    p1 = p1->next;
   }
  }
 }
 //检查有无负回路
  for(i=1;i<=n;i++)
  {
   edgeNode *p2 = adjlist[i].link;
   while(p2 != NULL)
   {
    if(lowcost[p2->no]>lowcost[i]+p2->weight)
     return false;
    p2 = p2->next;
   }
  }
 return true;
}

int _tmain(int argc, _TCHAR* argv[])
{
 int cases;
 cout<<"请输入案例的个数：";
 cin>>cases;
 while(cases--)
 {
  int i,j;
  int n,m;
  cout<<"请输入差分矩阵的行数(m)与列数(n)：";
  cin>>m>>n;
  cout<<"请输入差分矩阵："<<endl;
  for(i=1;i<=m;i++)
   for(j=1;j<=n;j++)
    cin>>a[i][j];
  cout<<"请输入约束集："<<endl;
  for(i=1;i<=m;i++)
   cin>>w[i];
  //创建邻接表
  createGraph(adjlist,parent,lowcost,w,m,n);
  //输出邻接表
  /*
  for(i=0;i<=n;i++)
  {
   edgeNode *p = adjlist[i].link;
   cout<<i<<":";
   while(p != NULL)
   {
    cout<<"("<<p->no<<","<<p->weight<<") ";
    p = p->next;
   }
   cout<<endl;
  }
  */
  //调用Bellman-Ford算法
  bool flag = Bellman_Ford(adjlist,lowcost,parent,n);
  if(!flag)
   cout<<"无解"<<endl;
  else
  {
   //输出解集
   cout<<"其中一个解集为（此解集加上一个任意的常数d也是其解集）："<<endl;
   for(i=1;i<=n;i++)
    cout<<"x"<<i<<"="<<lowcost[i]<<endl;
  }
 }
 system("pause");
 return 0;
}

---------------------------------------------------程序测试---------------------------------------------------                                       

请输入案例的个数：1
请输入差分矩阵的行数(m)与列数(n)：8  5
请输入差分矩阵：
1 -1 0 0 0
1 0 0 0 -1
0 1 0 0 -1
-1 0 1 0 0
-1 0 0 1 0
0 0 -1 1 0
0 0 -1 0 1
0 0 0 -1 1
请输入约束集：
0 -1 1 5 4 -1 -3 -3
其中一个解集为（此解集加上一个任意的常数d也是其解集）：
x1=-5
x2=-3
x3=0
x4=-1
x5=-4
请按任意键继续. . .