在阅读此文章之前,您需要了解BFS(广度优先搜索),邻接表存储方法,STL中的vector和queue,以及图论中的基本知识。
1. 什么是拓扑排序?
拓扑排序就是在一个有向无环图(也称DAG图),将所有的点排成一个线性的序列,使得每条有向边的起点u都排在终点v的前面。
关于AOV网:
假设一个有先决要求的任务为v,必须先要完成任务u,这时就可以建一条有向边,以u为起点,v为终点。通常,我们把这种点表示任务,边表示任务之间的前后顺序关系的有向图称为AOV网(Activity On Vertex network)。
如果您觉得上述比较难理解,可以举一个简单的例子。比如,在洛谷中的试炼场,有一些有先决要求的任务,这些任务必须要先完成其他的子任务才能做(不考虑直接跳过的情况),因此要先完成以前的子任务才能去做,有先解决任务的优先级要比它的子任务要高,这种关系可以用一个AOV网来表示任务之间的关系。
2.如何实现拓扑排序?
实现拓扑排序的方法在这里先介绍两种算法,DFS(深度优先搜索)以及(BFS广度优先搜索)。
我们先来谈谈如何用BFS的方法。
-
先建图。这里本蒟蒻采用的是邻接表方法。用C++STL中的vector(当然也可用链式前向星)。读入两个点u,v。u是起点,v是终点,将v插入u的vector中,即G[u].push_back(v);这样第一步就做好了qwq
-
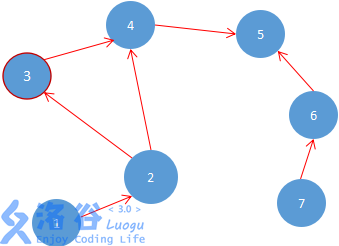
BFS实现拓扑排序。首先我们找图中所有入度为0的点。(入度就是一个点被指向边的数量,一个有向无环图中一定存在一个入度为0的点)。那怎样才能统计入度?很简单,只要在刚才建图的过程中,把每条边终点v的入度加1即可,把每个点的入度用一个一维数组来存储即可。如果您不是很理解,我们不妨先画一个图。
-
以上这幅图中通过观察发现入度为0的点为1和7(即没有边指向1与7),我们就把1号点和7号点放入一个队列当中,准备接下来的操作。学过BFS的同学都知道,一般写BFS的时候都要用到队列(数据结构队列在这里作者不在阐述)。
-
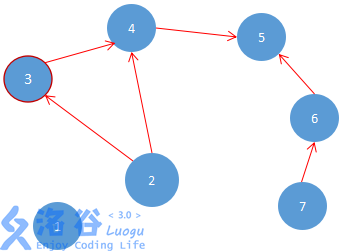
然后我们拿出队列中的首项v,并可以直接输出这个点的编号,因为现在的图中已经不存在一条边的终点是v,比它优先级高的点要么已经输出过了,要么就不存在,接着我们要对v做一次伟大的操作,就是把所有以它自己为起点的边全部删掉,如上图所示,如果v为1,就把从1至2的这条边删掉。变成了下图。
-
到这儿可能有同学会问,怎么才能把边删除掉呢?其实我们并不必要真正的把边删除,只要把每条边终点的入度减一就行了,这样可以代替删边的过程,这时我们还要继续判断,如果这是终点的入度为0(即删后没有边指向它了),那么我们就把这个点丢入队列中(做好下次输出并进行同样操作的准备)。
-
最后,一直重复以上的过程,直到所有边都删完(队列为空)时,整个用BFS拓扑排序的过程已经结束了。
-
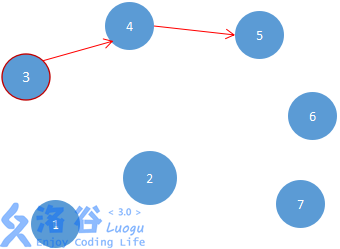
如果您不是很理解上述,我们再继续操作上面的图。此时已经输出了1,7,并把点2与点6丢进队列中。然后我们再拿出2进行操作,先输出2,把到点3和点4的边删掉(即删掉3,4点的入度),再将操作后入度为0的点3放进队列里,此时点2已经了结束操作。我们并把队列中剩下的点6拿出来,输出6,并删掉到点5的边,而5的入度并不等于0(还有起点是点4的边),所以不能把5放入队列中,此时6点结束操作。又变成了以下此图(现在已经输出了1,7,2,6)
-
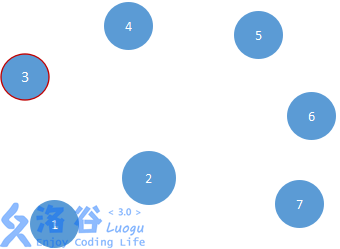
此时队列中只有点3。我们把它取出来,输出它的编号,并删掉到点4的边,并把点4放入队列。我们又双叒叕拿出队列中的首项(点4),并输出点的编号,然后在把到5的边删去,并把5放入队列。于是又变成了下图(目前拓扑排序为1,7,2,6,3,4):
-
此时图中所有边已经全部删完,但过程并没有结束,我们拿出点5并输出,发现没有从5开始的边,结束点5的操作。此时,队列为空,因此我们已经完成了此图整个拓扑排序的操作,最终的序列为:1,7,2,6,3,4,5。
下面送代码QwQ
-
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
#define MAXN 1010
int in[MAXN];//用来存每个点的入度总数
vector<int>G[MAXN];//vector数组,头文件是#include<vector>
void topsort(int n)
{
queue<int>q;//定义一个队列,头文件是#include<queue>
for(int i=1; i<=n; i++)
if(!in[i]) q.push(i);//如果这个点的入度为0,就进入队列
while(!q.empty())//当队列不为空时就进行
{
int v=q.front();//取出队中的首项
q.pop();//并拿出
cout<<v<<' ';//这时候可以输出v点了
for(int i=0; i<G[v].size(); i++)//做删边的操作
{
in[G[v][i]]--;//终点的入度减一
if(!in[G[v][i]])//如果终点入度为0
{
q.push(G[v][i]);//进入队列
}
}
}
}
int main()
{
int n,m;
cin>>n>>m;//读入
for(int i=1; i<=m; i++)
{
int u,v;
cin>>u>>v;
in[v]++;//v的入度+1
G[u].push_back(v);//建一条边
}
topsort(n);//拓扑排序
return 0;
}
如何在拓扑排序时判环?
如果有时这个图不是一个DAG,只是一个普通的有向图,这时我们拓扑排序时需要判环,简单画个有环的例子。

如上图所示,点2,3,4构成了一个环.怎样判断环呢,还是很简单的,按上面所说的过程运行,操作1节点时,发现3的入度并没有为0,而现在1节点已经退出了队列了,且另一个点2也到达不了,这样就永远也到达不了3了,只要出现这种情况我们就可以判断这个图就是一个存在环的有向图。那怎样去实现呢?只要在以上程序中的while循环中加一个tot计数器就OK了,每次从队列中拿出一个数时,tot加1,while循环结束的时候判断tot是否等于节点总数,若不等于,则说明图是有环的。
代码:
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
#define MAXN 1010
int in[MAXN];
vector<int>G[MAXN];
int ans[MAXN];//存答案的数组
void topsort(int n)
{
int tot=0,size=0;
queue<int>q;
for(int i=1; i<=n; i++)
if(!in[i]) q.push(i);
while(!q.empty())
{
int v=q.front();//取出队中的首项
q.pop();//并拿出
tot++;
ans[++size]=v;//这时不能输出了,因为可能存在环
for(int i=0; i<G[v].size(); i++)//做出牺牲,删边
{
in[G[v][i]]--;//终点的入度减一
if(!in[G[v][i]])//如果终点入度为0
{
q.push(G[v][i]);//进入队列
}
}
}
if(tot==n)
{
for(int i=1; i<=size; i++)
cout<<ans[i]<<' ';
}
else
{
cout<<"No";//有环
}
}
int main()
{
int n,m;
cin>>n>>m;//读入
for(int i=1; i<=m; i++)
{
int u,v;
cin>>u>>v;
in[v]++;//v的入读+1
G[u].push_back(v);//建一条边,vector
}
topsort(n);//拓扑排序
return 0;
}拓扑排序地正确使用方式.
拓扑排序大部分情况下都是和其他算法用在一起的,在拓扑排序的时候我们可以在里面写一个动态规划dp,也就是在图上dp,这样做可以避免在状态转移时新的状态没有计算的情况,这是一个很常见的套路。如果图是一个有向有环图,这时我们必须要先用Tarjan缩点后在拓扑排序。
拓扑排序的时间复杂度:
拓扑排序的时间复杂度是线性的,为O(N+M),M表示图中有向边的个数,N表示图中节点数,相对来说还是很快的。
有哪些拓扑排序的题目?
洛谷上的P3243(算是一道拓扑排序的水题,怕是假的紫题)
P1038 神经网络 一道很经典的拓扑排序题目
P2017 先拓扑排序单向道路,在比较每个双向道路起点终点的前后顺序
P4742 先用Tarjan缩点,然后用拓扑排序加dp,很常见的套路
PS:本人蒟蒻一枚,如果此文章有哪里说错了,欢迎在评论区里告诉作者qwq
呵呵呵呵呵







