原理为:原理:素数的倍数一抄定不是素数。
我们可以用一个长度为n+1的数组袭来存储信息(这种用另一个数组来保存信息的方法很常见也很有用),首先将所有的数百字全初始化为0(素数),再将数字1与第一个素数2标记为1(非素度数)从素数2开始将所有小于n的2的倍数都标记为1;继续该过程,知将素数3的倍数筛掉,道到循环结束时,标记仍为0的数就是素数。
前言
在刚接触编程语言时,对于寻找素数,第一时间想到的便是二重循环暴力查找,其复杂度O(n),通过循环中只判断到根号n可以优化一些,不过复杂度也达不到预期。在数论的学习中,我学到了埃氏筛法,O(nloglogn)的算法,而在一些数据范围达到1e7这样的题目中,也很难让人满意,于是我便学习了欧拉筛法,也即 O(n)的线性筛法。
埃氏筛法
埃氏筛法的基本思想 :从2开始,将每个质数的倍数都标记成合数,以达到筛选素数的目的。
代码 :
int visit[maxn];
void Prime(){
mem(visit,0); //初始化都是素数
visit[0] = visit[1] = 1; //0 和 1不是素数
for (int i = 2; i <= maxn; i++) {
if (!visit[i]) { //如果i是素数,让i的所有倍数都不是素数
for (int j = i*i; j <= maxn; j += i) {
visit[j] = 1;
}
}
}
这里有一个小优化,j 从 i * i 而不是从 i + i开始,因为 i*(2~ i-1)在 2~i-1时都已经被筛去,所以从i * i开始。
埃氏筛法的缺陷 :对于一个合数,有可能被筛多次。例如 30 = 2 * 15 = 3 * 10 = 5*6……那么如何确保每个合数只被筛选一次呢?我们只要用它的最小质因子来筛选即可,这便是欧拉筛法。
欧拉筛法
欧拉筛法的基本思想 :在埃氏筛法的基础上,让每个合数只被它的最小质因子筛选一次,以达到不重复的目的。
代码 :
int prime[maxn];
int visit[maxn];
void Prime(){
mem(visit,0);
mem(prime, 0);
for (int i = 2;i <= maxn; i++) {
cout<<" i = "<<i<<endl;
if (!visit[i]) {
prime[++prime[0]] = i; //纪录素数, 这个prime[0] 相当于 cnt,用来计数
}
for (int j = 1; j <=prime[0] && i*prime[j] <= maxn; j++) {
// cout<<" j = "<<j<<" prime["<<j<<"]"<<" = "<<prime[j]<<" i*prime[j] = "<<i*prime[j]<<endl;
visit[i*prime[j]] = 1;
if (i % prime[j] == 0) {
break;
}
}
}
}
对于visit[i*prime[j]] = 1 的解释: 这里不是用i的倍数来消去合数,而是把 prime里面纪录的素数,升序来当做要消去合数的最小素因子。
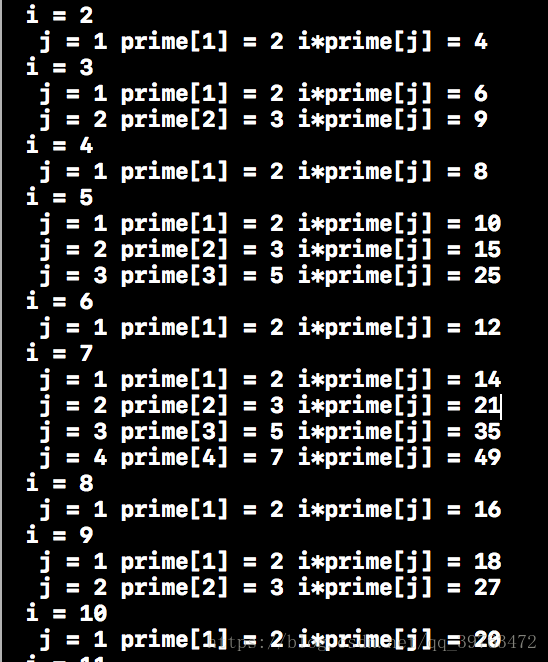
打表观察来理解 :
发现i在消去合数中的作用是当做倍数的。
对于 i%prime[j] == 0 就break的解释 :当 i是prime[j]的倍数时,i = kprime[j],如果继续运算 j+1,i * prime[j+1] = prime[j] * k prime[j+1],这里prime[j]是最小的素因子,当i = k * prime[j+1]时会重复,所以才跳出循环。
举个例子 :i = 8 ,j = 1,prime[j] = 2,如果不跳出循环,prime[j+1] = 3,8 * 3 = 2 * 4 * 3 = 2 * 12,在i = 12时会计算。因为欧拉筛法的原理便是通过最小素因子来消除。
李致远在2020-05-06 21:03:59追加了内容
我阔以告诉您@赵郎 虽然我们的内容甚至时间都一样,但这是我自己找的(请您相信我!OvO)
@丁博然 我不和您一个班呐
李致远在2020-05-06 21:05:45追加了内容
@丁博扬
@赵朗
我我我都@错了。。。